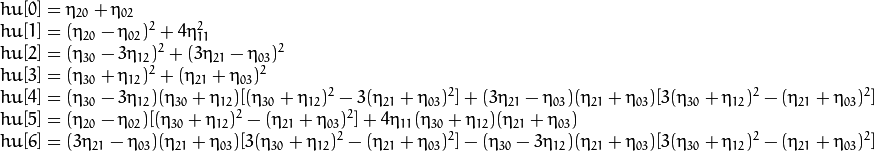１、几何矩理论

1.1 矩与数学期望

• 数学期望

定义（一维离散）：设X∈[a,b]$\mathbf{X}\in [a,b]$，密度为f(x)$f(x)$，数学期望为：

E(X)=∑i=1∞xiP(xi)$$E(X)=\sum _{i=1}^{\mathrm{\infty }}{x}_{i}P(x_i)$$

定义（一维连续）：设X$\mathbf{X}$为连续型随机变量，其概率密度为f(x)$f(x)$，则X的数学期望为：

E(X)=∫+∞−∞xf(x)dx$$E(X)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}xf(x)dx$$

注：假定广义积分绝对收敛，即∫+∞−∞|x|f(x)dx${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}|x|f(x)dx$存在

定义（二维离散）：对于离散变量(X,Y)$(\mathbf{X},\mathbf{Y})$的P(xi,yi)$P(x_i,y_i)$，PX(xi)=∑jP(xi,yj)$P_{\mathbf{X}}(x_i)=\sum _{j}P(x_i,y_j)$期望为：

E(X)=∑ixiPX(xi)=∑j∑ixiP(xi,yj)$$E(X)=\sum _i{x}_i{P}_{\mathbf{X}}(x_i)=\sum _j\sum _i{x}_{i}P(x_i,y_j)$$

E(Y)=∑jyjPY(yj)=∑j∑iyjP(xi,yj)$$E(Y)=\sum _j{y}_j{P}_{\mathbf{Y}}(y_j)=\sum _j\sum _i{y}_{j}P(x_i,y_j)$$

定义（二维连续）：连续变量(X,Y)$(\mathbf{X},\mathbf{Y})$的f(x,y)$f(x,y)$:

fX(x)=∫+∞−∞f(x,y)dy$$f_{\mathbf{X}}(x)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f(x,y)dy$$

E(X)=∫+∞−∞xfX(x)dx=∫+∞−∞x(∫+∞−∞f(x,y)dy)dx=∫+∞−∞∫+∞−∞xf(x,y)dxdy$$\begin{gathered} E(X)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}x{f}_{\mathbf{X}}(x)dx={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}x({\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f(x,y)dy)dx \\ ={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}xf(x,y)dxdy \end{gathered}$$

E(Y)=∫+∞−∞yfY(y)dy=∫+∞−∞∫+∞−∞yf(x,y)dxdy$$E(Y)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}y{f}_{\mathbf{Y}}(y)dy={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}yf(x,y)dxdy$$

• 原点矩

定义1：设X$\mathbf{X}$是随机变量，则称νk(X)=E(Xk)${\nu }_k(\mathbf{X})=E({\mathbf{X}}^k)$为X$\mathbf{X}$的k$k$阶原点矩。

若X$\mathbf{X}$是离散型随机变量，则：

νk(X)=∑ixkip(xi)$${\nu }_k(X)=\sum _i{x}_i^{k}p(x_i)$$

若X$\mathbf{X}$是连续型随机变量，则：

νk(X)=∫+∞−∞xkf(x)dx$${\nu }_k(X)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}{x}^{k}f(x)dx$$

• 中心距

定义2：设X$\mathbf{X}$是随机变量，则称

μk(X)=E(X−E(X))k$${\mu }_k(X)=E(\mathbf{X}-E(\mathbf{X}){)}^k$$

为 X$\mathbf{X}$的 k$k$阶中心距。

若X$\mathbf{X}$是离散型随机变量，则：

μk(X)=∑i(xi−E(X))kp(xi)$${\mu }_k(X)=\sum _i(x_i-E(X){)}^{k}p(x_i)$$

若X$\mathbf{X}$是连续型随机变量，则：

μk(X)=∫+∞−∞(x−E(X))kf(x)dx$${\mu }_k(X)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}(x-E(X){)}^{k}f(x)dx$$

• 原点矩与中心距

当中心距中的E(X)$E(\mathbf{X})$为0时，此时为k$k$阶原点矩，即原点矩是中心距的特殊情况。

一阶原点矩就是数学期望，二阶中心距就是方差，在实际中常用低阶矩，高于四阶矩极少使用。

原点矩与中心距的关系式：

以上可对μr${\mu }_r$用组合数拆开得到。

1.2 图像的矩

把图像的像素看做密度函数f(x,y)$f(x,y)$，对该像素点求期望E$E$，即是图像的矩（原点矩）。具体的求解过程参看下面第2节。

一般来说，一阶矩和零阶矩可以计算某个形状的重心，二阶矩可以计算形状的方向。

图像的矩主要表征了图像区域的几何特征，又称几何矩，由于具有旋转、平移、尺度等不变的特兴奋，所以又称为不变矩。
利用不变矩可以计算出物体的圆形度（物体形状和园的接近程度）、物体的矩形度（物体形状和矩形的接近程度）、物体的水平和垂直对称性、物体的主轴方向、扁度等。

• 原点矩：
  

  mpq=∑x−1M∑y−1Nxpyqf(x,y)$$m_{pq}=\sum _{x-1}^M\sum _{y-1}^N{x}^p{y}^{q}f(x,y)$$

  
  

• moments of a patch(矩):
  

  mpq=∑x=−r,y=−rrxpyqI(x,y)(1)$$\begin{array}{}\text{(1)}& m_{pq}=\sum _{x=-r,y=-r}^r{x}^p{y}^{q}I(x,y)\end{array}$$

  
  

• 角点为中心：
  

  m00=∑x=−r,y=−rrx0y0I(x,y)=∑x=−r,y=−rrI(x,y)(1-1)$$\begin{array}{}\text{(1-1)}& m_{00}=\sum _{x=-r,y=-r}^r{x}^0{y}^{0}I(x,y)=\sum _{x=-r,y=-r}^{r}I(x,y)\end{array}$$

  
  

• 一阶矩m01$m_{01}$:
  

  m01=∑x=−r,y=−rrx0y1I(x,y)=∑x=−r,y=−rry∗I(x,y)(1-2)$$\begin{array}{}\text{(1-2)}& m_{01}=\sum _{x=-r,y=-r}^r{x}^0{y}^{1}I(x,y)=\sum _{x=-r,y=-r}^{r}y\ast I(x,y)\end{array}$$

  
  

• 一阶矩m10$m_{10}$:
  

  m10=∑x=−r,y=−rrx1y0I(x,y)=∑x=−r,y=−rrx∗I(x,y)(1-3)$$\begin{array}{}\text{(1-3)}& m_{10}=\sum _{x=-r,y=-r}^r{x}^1{y}^{0}I(x,y)=\sum _{x=-r,y=-r}^{r}x\ast I(x,y)\end{array}$$

  
  

• centroid（质心，亦可称为重心）：
  

  C=(m10m00,m01m00)(2)$$\begin{array}{}\text{(2)}& C=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}})\end{array}$$

  
  计算质心的优势：对噪声不敏感。当有外部噪声干扰时，计算出的质心不会偏离太大。从数学的角度来看，这种方法是计算一个连通域的质心（或一个团块儿blob的质心）。

  
  

• 构造一个向量OC−→−$\overrightarrow{OC}$,从角点中心O$O$到质心C$C$。

• orientation of patch（方向）：
  

  θ=atan2(m01,m10)(3)$$\begin{array}{}\text{(3)}& \theta =atan2(m_{01},m_{10})\end{array}$$

  
  建立以角点为圆心的坐标系，如图
  在图中，P$P$为角点，园内为取点区域，每个方格代表一个像素。
  则质心Q$Q$可根据式（2）求得。

  
  

• moments()

• The function computes moments, up to the 3rd order, of a vector shape or a rasterized shape. The results are returned in the structure Moments defined as:

• 1

• 2

• 3

• 4

• 5

• 6

• 7

• 8

• 9

• 10

• 11

• 12

• 13

• 14

• 15

• 16

• opencv2.4.13

• 1

• 2

• 3

• 4

• 5

• 6

• 7

• 8

• 9

• 10

• 11

• 12

• 13

• 14

• 15

• 16

• 17

• 18

• 19

• 20

• 21

• 22

• 23

• 24

• 25

• 26

• 27

• 28

• 29

• 30

• 31

• 32

• 33

• 34

• 35

• 36

• 37

• 38

• 39

• 40

• 41

• 42

• 43

• 44

• 45

• 46

• 47

• 48

• 49

• 50

• 51

• 52

• 53

• 54

• 55

• 56

• 57

• 58

• 59

• 60

• 61

• 62

• 63

• 64

• 65

• 66

• 67

• 68

• 69

• 70

• 71

• 72

• 73

• 74

• 75

• 76

• 77

• 78

• 79

• 80

• 81

• 82

• 83

• 84

• 85

• 86

• 87

• 88

• 89

• 90

• 91

• 92

• 93

• 94

• 95

• 96

• 97

• 98

• 99

• 100

• 101

• 102

• 103

• 1

• 2

• 3

• 4

• 5

• 6

• 7

• 8

• 9

• 10

• 11

• 12

• 13

• 14

• 15

• 16

• 17

• 18

• 19

• 20

• 21

• 22

• 23

• 24

• 25

• 26

• 27

• 28

• 29

• 30

• 31

• 32

• 33

• 34

• 35

• 36

• 37

• 38

• 39

• 40

• 41

• 42

• 43

• 44

• 45

• 46

• 47

• 48

• 49

• 50

• 51

• 52

• 53

• 54

• 55

• 56

• 57

• 58

• 59

• 60

• 61

• 
  

• 参考：
  

• 中心距：
  

  μpq=∑x−1M∑y−1N(x−x0)p(y−y0)qf(x,y)$${\mu }_{pq}=\sum _{x-1}^M\sum _{y-1}^N(x-x_0{)}^p(y-y_0{)}^{q}f(x,y)$$

  
  

• 归一化中心距：
  

  ηpq=μpqμr00$${\eta }_{pq}=\frac{{\mu }_{pq}}{{\mu }_{00}^r}$$

  
  其中r=p+q+22,p+q=2,3,...$r=\frac{p+q+2}{2},p+q=2,3,...$

  
  

• 一阶矩：
  见下面第２节．

• 二阶矩：

• 
  

  M20=∑x∑yx2⋅I(x,y)$$M_{20}=\sum _x\sum _y{x}^2·I(x,y)$$

  
  

  
  

  M02=∑x∑yy2⋅I(x,y)$$M_{02}=\sum _x\sum _y{y}^2·I(x,y)$$

  
  

  
  

  M11=∑x∑yx⋅y⋅I(x,y)$$M_{11}=\sum _x\sum _{y}x·y·I(x,y)$$

  
  

  M20$M_{20}$和M02$M_{02}$分别表示图像围绕通过重心的垂直和水平轴线的惯性矩。
  M30$M_{30}$和M03$M_{03}$可以度量图像对于垂直和水平轴线的对称性等。

  物体形状的方向：
  

  θ=arctan(b,(a−c))2=arctan(b/(a−c))2,θ∈[−90。，90。]$$\theta =\frac{arctan(b,(a-c))}{2}=\frac{arctan(b/(a-c))}{2},\theta \in [-{90}^{。}，{90}^{。}]$$

  
  其中：

  
  

  根据一阶矩的质心C=(M10M00,M01M00)$C=(\frac{M_{10}}{M_{00}},\frac{M_{01}}{M_{00}})$有

  
  

  a=M20M00−C20$$a=\frac{M_{20}}{M_{00}}-C_0^2$$

  
  

  
  

  b=2(M11M00−C0C1)$$b=2(\frac{M_{11}}{M_{00}}-C_0{C}_1)$$

  
  

  
  

  c=M02M00−C21$$c=\frac{M_{02}}{M_{00}}-C_1^2$$

  
  

  2、质心原理

  在图像处理中，一阶矩与形状有关，二阶矩显示曲线围绕直线平均值到扩展程度，三阶矩是关于平均值到对称性到测量．由二阶矩和三阶矩可以导出一组共７个不变矩．而不变矩是图像到统计特性，满足平移，伸缩，旋转均不变到不变性．

  ---

  3、中心距函数moments()

  Calculates all of the moments up to the third order of a polygon or rasterized shape.

  C++: Moments moments(InputArray array, bool binaryImage=false )

  Python: cv2.moments(array[, binaryImage]) → retval

  C: void cvMoments(const CvArr* arr, CvMoments* moments, int binary=0 )

  Python: cv.Moments(arr, binary=0) → moments

  Parameters:
  array – Raster image (single-channel, 8-bit or floating-point 2D array) or an array ( 1 \times N or N \times 1 ) of 2D points (Point or Point2f ).
  binaryImage – If it is true, all non-zero image pixels are treated as 1’s. The parameter is used for images only.
  moments – Output moments.

  class Moments
  {public:    Moments();
      Moments(double m00, double m10, double m01, double m20, double m11,            double m02, double m30, double m21, double m12, double m03 );
      Moments( const CvMoments& moments );    operator CvMoments() const;    // spatial moments
      double  m00, m10, m01, m20, m11, m02, m30, m21, m12, m03;    // central moments
      double  mu20, mu11, mu02, mu30, mu21, mu12, mu03;    // central normalized moments
      double  nu20, nu11, nu02, nu30, nu21, nu12, nu03;
  }

  ---

  4、中心矩示例代码

  4.1 C++版代码

  #include <QCoreApplication>#include <opencv2/opencv.hpp>//  Qt Creator 4.2.0(Based on Qt 5.7.1)//  OpenCV 2.4.13using namespace cv;using namespace std;#define name1 "原图"#define name2 "效果图"cv::Mat img, gray;int nThresh = 100;int nMaxThresh = 255;
  cv::RNG rng(12345);  //产生一个随机数cv::Mat cannyImg;std::vector<std::vector<cv::Point>> contours;std::vector<cv::Vec4i> hierarchy;//void on_ThreshChange( int, void* ){//    //canny边缘检测//    cv::Canny( gray, cannyImg, nThresh, nThresh*2, 3 );//    //找轮廓//    cv::findContours( cannyImg, contours, hierarchy, cv::RETR_TREE, cv::CHAIN_APPROX_SIMPLE, cv::Point( 0, 0 ) );//    //计算矩//    std::vector<cv::Moments> mu( contours.size() );//    for(unsigned int i = 0; i < contours.size(); i++){//        mu[i] = cv::moments( contours[i], false);//    }//    //计算中心矩//    std::vector<cv::Point2f> mc( contours.size() );//    for( unsigned int i = 0; i < contours.size(); i++ ){//        mc[i] = cv::Point2f( static_cast<float>(mu[i].m10 / mu[i].m00), static_cast<float>(mu[i].m01 / mu[i].m00));//    }//    //画轮廓//    cv::Mat drawing = cv::Mat::zeros( cannyImg.size(), CV_8UC3);//    for( unsigned int i = 0; i < contours.size(); i++ ){//        cv::Scalar color = cv::Scalar( rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255) );//        cv::drawContours( drawing, contours, i, color, 2, 8, hierarchy, 0, cv::Point() );//        cv::circle( drawing, mc[i], 4, color, -1, 8, 0 );//    }//    cv::namedWindow( name2, cv::WINDOW_NORMAL);//    cv::imshow( name2, drawing );//    std::cout << "输出内容：　面积和轮廓长度　\n" << std::endl;//    for(unsigned int i = 0; i < contours.size(); i++ ){//        std::cout << ">通过ｍ00计算出轮廓[" << i << "]的面积：(M_00) =" << mu[i].m00 << "\n OpenCV 函数计算出的面积　＝　" << cv::contourArea(contours[i]) << "长度：" << cv::arcLength( contours[i], true) <<  "\n\n" << std::endl;//        cv::Scalar color = cv::Scalar( rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255) );//        cv::drawContours(drawing, contours, i, color, 2, 8, hierarchy, 0, cv::Point() );//        cv::circle( drawing, mc[i], 4, color, -1, 8, 0 );//     }//}int main(){
      img = cv::imread( "/home/jason/jason2/photo/1.jpg" );
      cv::cvtColor( img, gray, cv::COLOR_BGR2GRAY );
      cv::blur( gray, gray, cv::Size(3, 3) );
  
      cv::namedWindow( name1, cv::WINDOW_NORMAL );
      cv::imshow( name1, img );//    cv::createTrackbar( "阈值", name1, &nThresh, nMaxThresh, on_ThreshChange );//    on_ThreshChange( 0, 0 );
  
      //canny边缘检测
      cv::Canny( gray, cannyImg, nThresh, nThresh*2, 3 );    //找轮廓
      cv::findContours( cannyImg, contours, hierarchy, cv::RETR_TREE, cv::CHAIN_APPROX_SIMPLE, cv::Point( 0, 0 ) );    //计算矩
      std::vector<cv::Moments> mu( contours.size() );    for(unsigned int i = 0; i < contours.size(); i++){
          mu[i] = cv::moments( contours[i], false);
      }    //计算中心矩
      std::vector<cv::Point2f> mc( contours.size() );    for( unsigned int i = 0; i < contours.size(); i++ ){
          mc[i] = cv::Point2f( static_cast<float>(mu[i].m10 / mu[i].m00), static_cast<float>(mu[i].m01 / mu[i].m00));
      }    //画轮廓
      cv::Mat drawing = cv::Mat::zeros( cannyImg.size(), CV_8UC3);    for( unsigned int i = 0; i < contours.size(); i++ ){
          cv::Scalar color = cv::Scalar( rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255) );
          cv::drawContours( drawing, contours, i, color, 2, 8, hierarchy, 0, cv::Point() );
          cv::circle( drawing, mc[i], 4, color, -1, 8, 0 );
      }
  
      cv::namedWindow( name2, cv::WINDOW_NORMAL);
      cv::imshow( name2, drawing );    std::cout << "输出内容：　面积和轮廓长度　\n" << std::endl;    for(unsigned int i = 0; i < contours.size(); i++ ){        std::cout << ">通过ｍ00计算出轮廓[" << i << "]的面积：(M_00) =" << mu[i].m00 << "\n OpenCV 函数计算出的面积　＝　" << cv::contourArea(contours[i]) << "长度：" << cv::arcLength( contours[i], true) <<  "\n\n" << std::endl;
          cv::Scalar color = cv::Scalar( rng.uniform(0, 255), rng.uniform(0, 255), rng.uniform(0, 255) );
          cv::drawContours(drawing, contours, i, color, 2, 8, hierarchy, 0, cv::Point() );
          cv::circle( drawing, mc[i], 4, color, -1, 8, 0 );
       }
      cv::waitKey(0);    return 0;
  }

  原图：
  

  效果图：
  

  部分打印结果：
  

  ---

  4.2 Python版代码

  # -*- coding: utf-8 -*-"""
  Created on Sun Mar 26 18:36:19 2017
  
  @author: lql0716
  """import cv2import numpy as np
  
  nThresh = 100nMaxThresh = 255img = cv2.imread('D:/photo/04.jpg')
  gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
  gray = cv2.blur(gray, (3,3))
  cv2.namedWindow('img', cv2.WINDOW_NORMAL)
  cv2.imshow('img', img)
  
  cannyImg = cv2.Canny(gray, nThresh, nThresh*2, 3)
  contours, hierarchy = cv2.findContours(cannyImg, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)
  
  mu = []
  mc = []
  retval = np.array([])for i in range(0, np.array(contours).shape[0]):
      retval = cv2.moments(contours[i], False)
      mu.append(retval)
  mu = np.array(mu)#print mu[0]['m10']thetas = []for i in range(0, np.array(contours).shape[0]):    if mu[i]['m00'] == 0.0:
          a=0
          b=0
      else:
          a = mu[i]['m10'] / mu[i]['m00']  #质心x坐标
          b = mu[i]['m01'] / mu[i]['m00']  #质心y坐标
  
          #根据二阶矩计算物体形状的方向
          r1 = mu[i]['m20'] / mu[i]['m00'] - a*a
          r2 = 2.0*(mu[i]['m11'] / mu[i]['m00'] - a*b)
          r3 = mu[i]['m02'] / mu[i]['m00'] - b*b#        print r1-r3
          if r1-r3==0:
              theta = np.pi / 2
          else:
              theta = np.arctan(r2/(r1-r3)) / 2
          thetas.append(theta)
      mc.append([a,b])
  mc = np.array(mc)
  drawing = np.zeros(img.shape, dtype = np.uint8)for i in range(0, mc.shape[0]):
      c1 = np.random.randint(0, 256)
      c2 = np.random.randint(0, 256)
      c3 = np.random.randint(0, 256)
      cv2.drawContours(drawing, contours, i, (c1, c2, c3), 2, 8)
      cv2.circle(drawing, (int(round(mc[i][0])), int(round(mc[i][1]))), 4, (c1, c2, c3), -1, 8, 0)
  cv2.namedWindow('img2', cv2.WINDOW_NORMAL)
  cv2.imshow('img2', drawing)   
  cv2.waitKey(0)

  原图：
  

  效果图：
  

  5、Hu矩HuMoments()

  原点矩：

  
  

  mpq=∑x−1M∑y−1Nxpyqf(x,y)$$m_{pq}=\sum _{x-1}^M\sum _{y-1}^N{x}^p{y}^{q}f(x,y)$$

  
  

  中心距：

  
  

  μpq=∑x−1M∑y−1N(x−x0)p(y−y0)qf(x,y)$${\mu }_{pq}=\sum _{x-1}^M\sum _{y-1}^N(x-x_0{)}^p(y-y_0{)}^{q}f(x,y)$$

  
  

  归一化中心距：

  
  

  ηpq=μpqμr00$${\eta }_{pq}=\frac{{\mu }_{pq}}{{\mu }_{00}^r}$$

  
  其中 r=p+q+22,p+q=2,3,...$r=\frac{p+q+2}{2},p+q=2,3,...$

  
  

  当图像变化时，mpq$m_{pq}$也变化，而μpq${\mu }_{pq}$具有平移不变形，但对旋转依然敏感。如果用归一化中心距，则可以保持平移不变性、伸缩不变性。

  Hu矩利用二阶、三阶中心距构造了7个不变矩，它们在连续图像条件下可保持平移、旋转、伸缩不变，公式如下：
  M1=η20+η02$M_1={\eta }_{20}+{\eta }_{02}$
  M2=(η20−η02)2+4η211$M_2=({\eta }_{20}-{\eta }_{02}{)}^2+4{\eta }_{11}^2$
  M3=(η30−3η12)2+(3η21−η03)2$M_3=({\eta }_{30}-3{\eta }_{12}{)}^2+(3{\eta }_{21}-{\eta }_{03}{)}^2$
  M4=(η30+η12)2+(η21+η03)2$M_4=({\eta }_{30}+{\eta }_{12}{)}^2+({\eta }_{21}+{\eta }_{03}{)}^2$
  M5=(η30−3η12)(η30+η12)((η30+η12)2−3(η21+η03)2)+(3η21−η03)(η21+η03)(3(η30+η12)2−(η21+η03)2)$M_5=({\eta }_{30}-3{\eta }_{12})({\eta }_{30}+{\eta }_{12})(({\eta }_{30}+{\eta }_{12}{)}^2-3({\eta }_{21}+{\eta }_{03}{)}^2)+(3{\eta }_{21}-{\eta }_{03})({\eta }_{21}+{\eta }_{03})(3({\eta }_{30}+{\eta }_{12}{)}^2-({\eta }_{21}+{\eta }_{03}{)}^2)$
  M6=(η20−η02)((η30+η12)2−(η21+η03)2)+4η11(η30+η12)(η21+η03)$M_6=({\eta }_{20}-{\eta }_{02})(({\eta }_{30}+{\eta }_{12}{)}^2-({\eta }_{21}+{\eta }_{03}{)}^2)+4{\eta }_{11}({\eta }_{30}+{\eta }_{12})({\eta }_{21}+{\eta }_{03})$
  M7=(3η21−η03)(η30+η12)((η30+η12)2−3(η21+η03)2)−(η30−3η12)(η21+η03)(3(η30+η12)2−(η21+η03)2)$M_7=(3{\eta }_{21}-{\eta }_{03})({\eta }_{30}+{\eta }_{12})(({\eta }_{30}+{\eta }_{12}{)}^2-3({\eta }_{21}+{\eta }_{03}{)}^2)-({\eta }_{30}-3{\eta }_{12})({\eta }_{21}+{\eta }_{03})(3({\eta }_{30}+{\eta }_{12}{)}^2-({\eta }_{21}+{\eta }_{03}{)}^2)$

  以下公式为官方文档的公式：
  

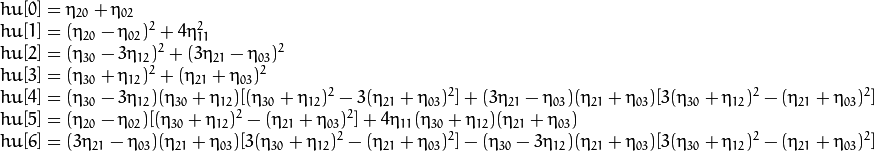
  在对图片识别过程中，只有M1$M_1$和M2$M_2$不变性保持的比较好，其他几个不变矩带来的误差比较大，有学者认为只有基于二阶矩的不变矩对二维物体的描述才真正具有旋转，缩放，平移不变性（M1$M_1$和M2$M_2$均为二阶矩构成）．

  Hu矩的优势：速度快
  Hu矩的劣势：识别率低

  Hu矩一般用来识别图像中大的物体，对物体的形状描述得比较好，图像的纹理特征不能太复杂，如识别水果形状或车牌字符的效果较好．

  
  

  
  

  1、图像的几何矩浅析
  2、opencv官方文档－moments()
  3、形状描述与识别
  4、第三章 二值图像分析

本文转载自：https://blog.csdn.net/lql0716/article/details/68267829

本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：