少有人走的路

三角函数里有许多公式，需要牢牢记住的只有6个，其它的都是其的变形。

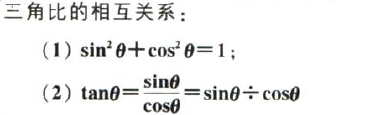
证明公式（1）：

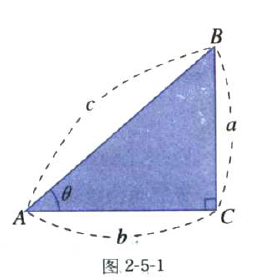
 a²+b²=c²

a²/c²+b²/c²=1

(a/c)²+(b/c)²=1

假设∠A=θ ，则a/c=sinθ, b/c=cosθ

∴  sin²θ+cos²θ=1

证明公式（2）

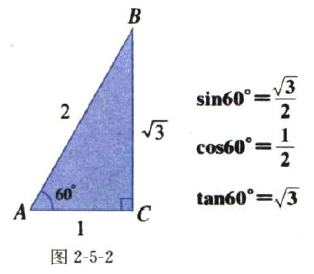
利用60°度直角可以验证公式（2）

tanθ=sinθ/cosθ

tan60°=sin60°/cos60°=(√3/2)/(1/2)=√3

下面来证明公式（2）

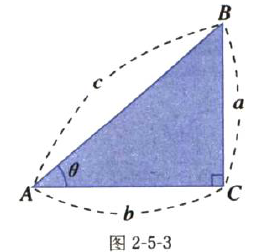
tanθ=a/b

tanθ=(a/c)/(b/c)

∴ tanθ=sinθ/cosθ

变形公式： tan² θ+1=1/cos²θ

它是公式（1）的变形：

推导如下：

sin²θ+cos²θ=1

两边式子除以cos²θ

sin²θ/cos²θ+1＝1/cos²θ

因为： tanθ=sinθ/cosθ

∴  tan²θ+1＝1/cos²θ

利用斜边长为1的直角三角形可以很容易证明公式1和公式2

按上面的公式（1）的证明方法，是三平方定理等式两边同时除以斜边的平方。

因为 BC²+AC²=AB²

BC²/AB²+AC²/AB²=AB²/AB²

假设∠A=θ，则

sin²θ+cos²θ=1

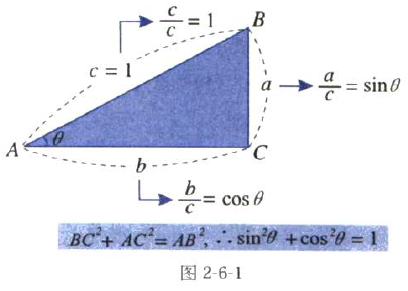
现在换个思路，如图2-6-1所示，假设RtΔABC的斜边为1，那么其它两边就是sinθ和cosθ,

把这三个边长的数值代入三平方定理，得得到公式（1）。

我们再把它们代入tanθ的公式，就得到了公式（2）

tabθ=CB/AC=sinθ/cosθ

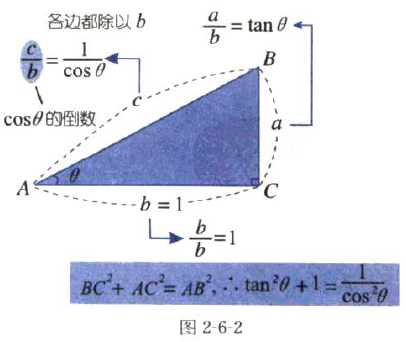
见下图2-6-2，如果假设θ的邻边b=1，则直角边a就是tanθ, 而斜边c就是1/cosθ。

把它们代入三平方定理就得

tan²θ+1=1/cos²θ

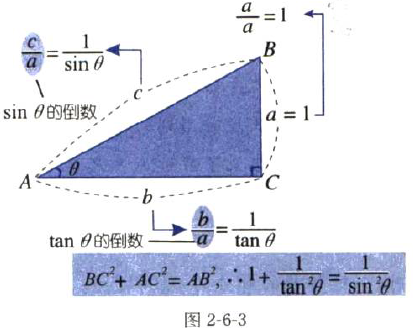
如下图，如果θ的对边a=1，则可以按上述思路推导出：

1+1/tan²θ=1/sin²θ

sinθ,cosθ,tanθ的倒数

这几个导数其实有另外的固定名称。

1/sinθ=cscθ,  1/cosθ=secθ,  1/tanθ=cotθ

这样式子 1+1/tan²θ=1/sin²θ 可以改写成：

1+cot²θ=csc²θ

--------------------- 

作者：hackpig
来源：www.skcircle.com
版权声明：本文为博主原创文章，转载请附上博文链接！