少有人走的路

手眼关系一般分为固定相机和移动相机两种模式。

在这章我们同样需要涉及到标定这块的知识，我们回顾一下，标定的流程一般如下：

图7.1.1 标定流程图

根据摄像机和机器人的位置关系可以分为Eye-in-Hand和eye-to-Hand。

摄像机安装在机械手上，并且随着机械手一起运动，这种称为Eye-in-Hand。

将摄像机安装在机械手本体之外，固定在某个位置，这种称为eye-to-hand。

机械手一般分为串联六轴的和四轴并联的，两种机械手的坐标系关系以及优势都不相同。

手眼标定的过程其实就是求解摄像机坐标系和机器人坐标系之间的转换关系。

我们先拿串联机械手来说，首先要确认四个坐标系：基础坐标系、机械手坐标系、摄像机坐标系、标定板坐标系。

那么当我们识别到物体后，其实就是进行各个坐标系的转换，从而引导机械手的未端执行机构进行抓取。

各个坐标系的转换主要是求解旋转矩阵和平移矢量，下面看下固定相机和移动式相机时的示意图。

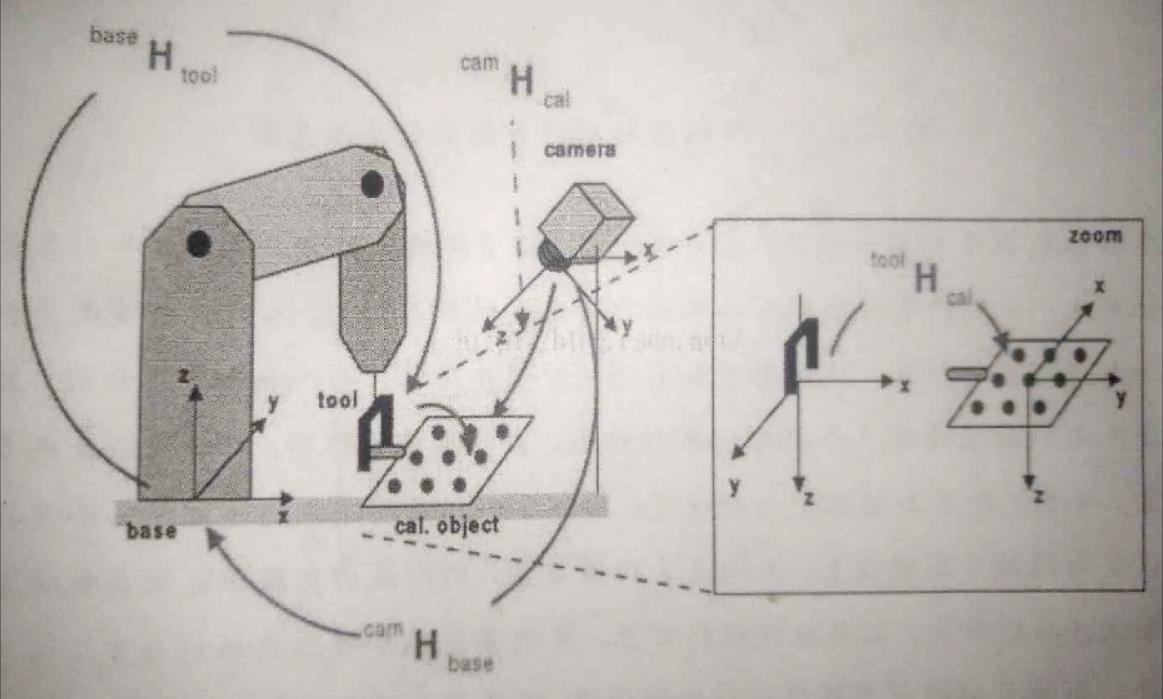
图7.1.2 相机固定的串联坐标系示意图

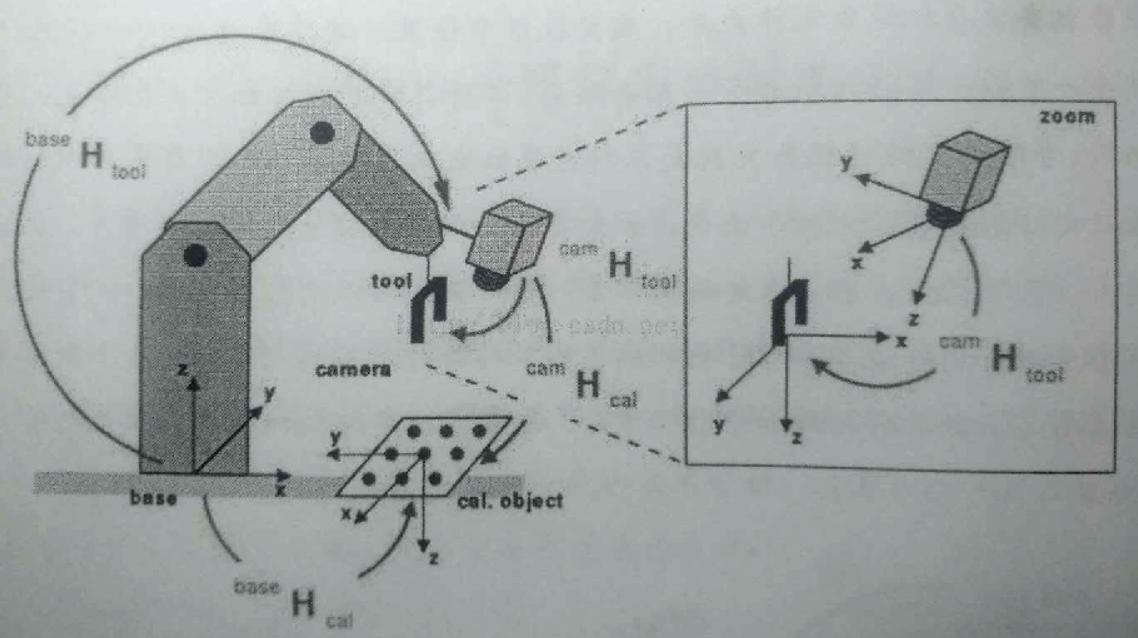
图7.1.3 相机移动时的串联坐标系示意图

在计算机视觉应用于机器人技术时，我们经常将摄像机固定在机械手的未端执行机构上，其目的是当机器人的未端执行器在抓取工件时，由摄像机去测定执行器与工件的相对位置，这种配置相当于眼睛放在手上。

与人和动物不相同，其原因是人与动物眼睛有一个很好的转动机制。

当人去抓取物体时，眼睛可以注视手的位置，并且判断手与物体的相对位置，而机器人要做到这点需要配置一个灵活的转台实时跟踪手抓的位置，做到这点比较复杂，所以我们把摄像机放在机械手上，手抓移动到哪里，摄像机就跟到哪里，并测量手抓和目标的相对位置。

由于机械手控制器可以控制手抓移动到任何位置，以使得手抓能够抓取物体的姿态与位置。

当手抓还没有到这个方位时，机器人必须知道物体相对于平台基础坐标系的位置，这个相对位置应该由摄像机测定出来。

将物体坐标系看成世界坐标系，物体相对于摄像机坐标系的位置就是相机的外参，这个外参我们可以用摄像机标定的方法计算出来。

如果此时还知道摄像坐标系相对于平台坐标系的位置，那么物体相对于摄像机坐标系的位置就可以转换成相对于平台坐标系的位置了，这就是机器人最后要的数据。

当摄像机固定在某个位置时，情况是比较简单的，因为摄像机坐标系相对于平台坐标系的位置是固定的，只要知道物体相对于摄像机坐标系的位置，也就是只要求摄像机内外参数，然后再根据摄像机相对于平台坐标系的固定位置就可以求出物体在平台坐标系下的位置，最后机器人控制器发送指令控制机械手到求出的位置去抓取。

如果相机固定在机械手上就要复杂点，需要实时对测量相机的外参确定物体相对于摄像坐标系的位置。

这就是整个手眼配合的过程。另外无论是静态抓取还是在有一定速度的传送带上抓取都是这样的流程。

手眼标定的核心其实就是坐标系转换，就是各种旋转与平移，这里对摄像机在机械手上的标定理论做一个简单的描述，先看下面的两个坐标系：

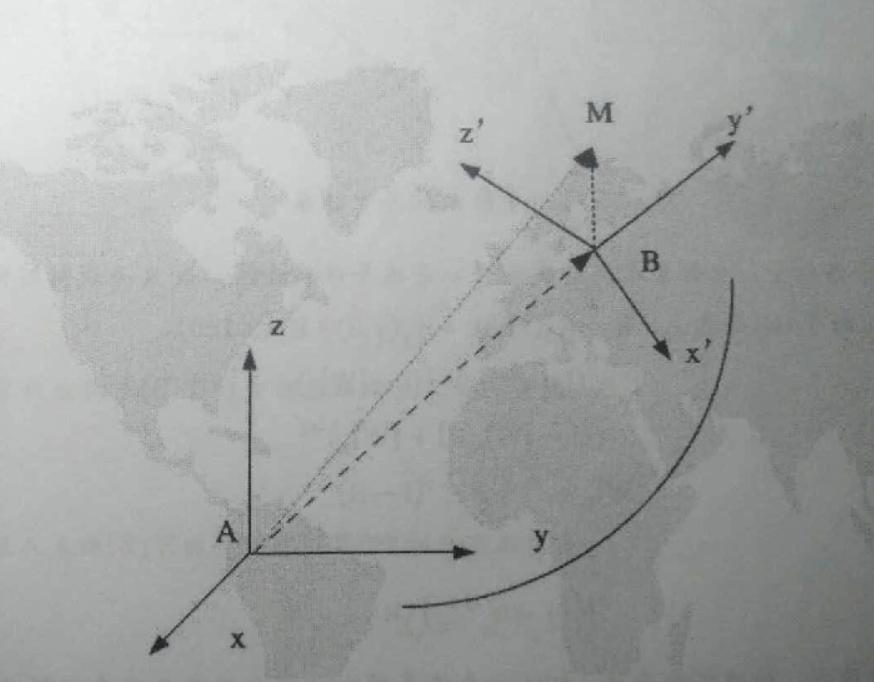
图7.1.4 坐标系转换简图

M点在A-xyz坐标系下的坐标为(x,y,z)，在B-x'y'z'下的坐标为(x',y',z')，两个坐标系原点之间的关系为AB，两个坐标系的关系为：

图7.1.5 串联机械手坐标系

T为平移向量，坐标系之间的变换可以看成平移和旋转，设R为旋转矩阵，R为{E}相对于{W}的姿态，R=R_z(z,90)*R_y(y,0)*R_x(x,180)

R=(1+[W]_x)^-1(1-[W]_x)

=(1-[W]_x)(1+[W]_x)^-1

[W]_x=(1+R)^-1(1-R)

=(1-R)(1+R)^-1

W=tan(θ/2).K

这里摄像机，执行机构未端，机械手本体基础坐标之间存在着来回转换的关系，摄像机固定的时候要简单一些

而摄像机跟踪执行机构一起运动的时候则更为复杂一些，需要实时知道它们的变换关系。

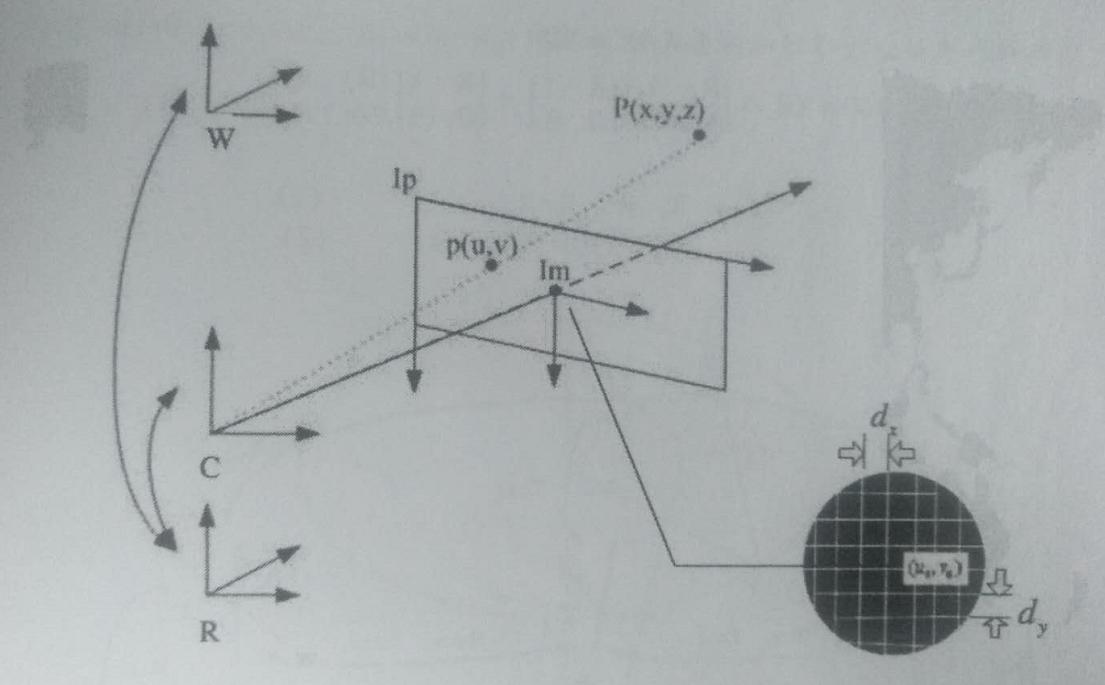
图7.1.6

摄像机坐标系{C}下的坐标与图像点之间的关系：

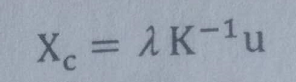
机器人未端{R}下的坐标与{C}下坐标之间的关系：

世界坐标系{W}下的坐标与{R}下坐标之间的关系：

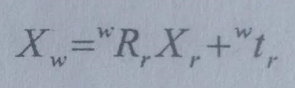
图像点与世界坐标系{W}下的坐标之间的关系：

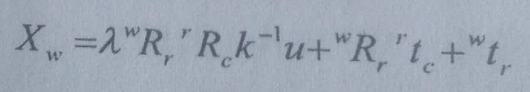
大家可以看到，其实每次坐标系转换的都是经过平移和旋转得到的。

所以整个过程的关键就是求每次运动后的旋转矩阵和平移矢量，那么求解这两个参数的方法有很多种，这里阐述传统的两步法求解。

经典的AX=XB求解方法：

K已知，先求R，后求t。

机器人运动一次得到的关系式AX=XB

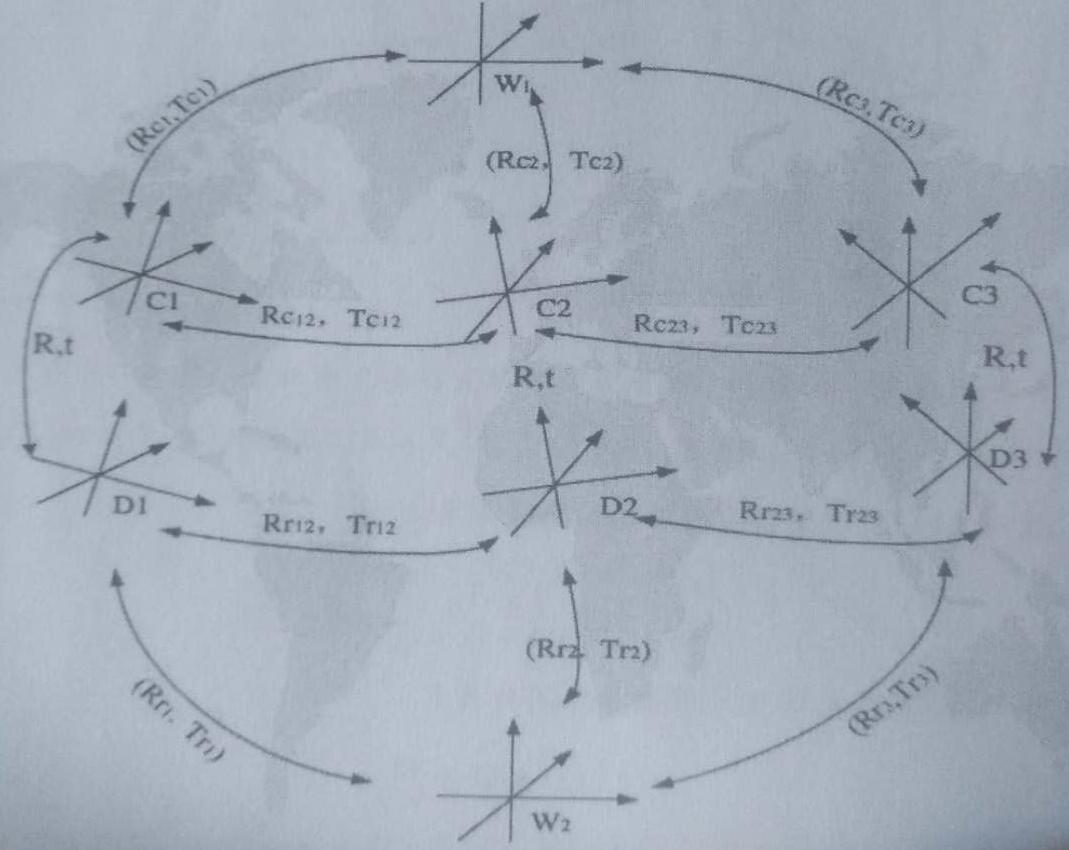
图7.1.7 运动关系图

求R：

利用Rodrigues表示旋转矩阵，即R=Rot(K,θ )

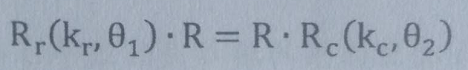
k_r和k_c分别是R_r和R_c的旋转轴，也是它们的特征值对应的特征向量，  θ₁和θ₂分别是旋转角。

由上式得到两个推论：

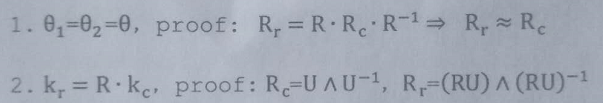
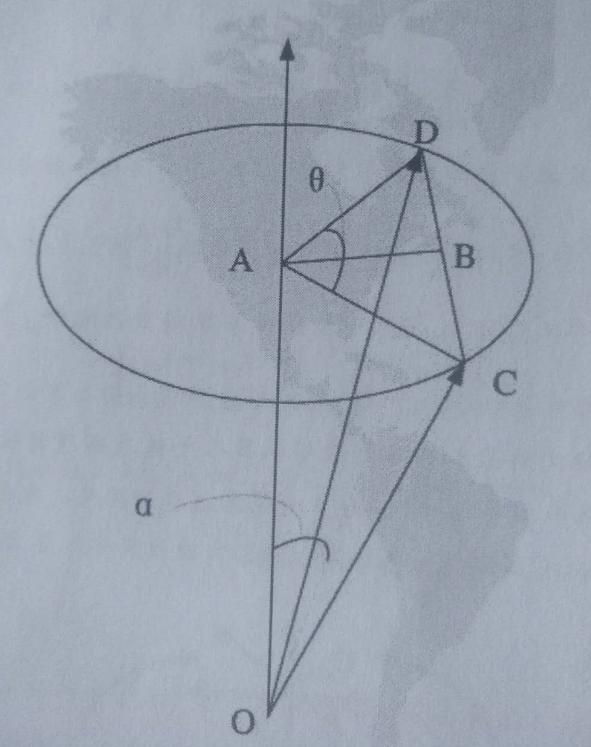
图7.1.8

根据上图得到几个关系：

R求解步骤：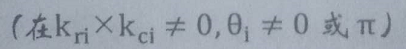

机器人手眼标定的基本思路是控制机器人手抓在不同的位置观察 空间一个已知的标 定物，从而推导R和t与多次观察结果的关系。

我们假设机器人平台从位置Pa移动到Pb时的各坐标位置关系。

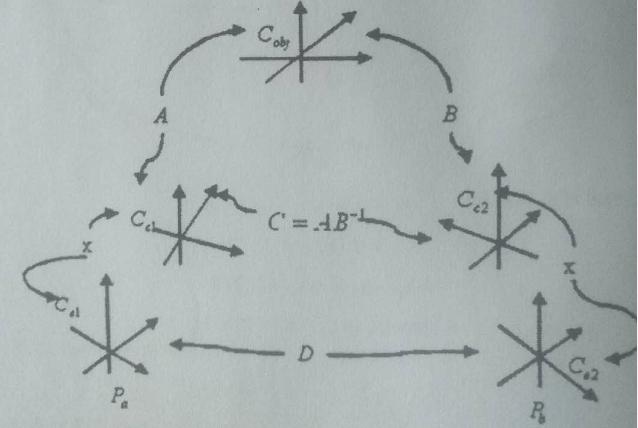
图7.1.9

C_obj为空间某物体的坐标系，C_c为摄像机坐标系，C_e为机器人未端执行器的坐标系。

我们可以用摄像机标定的方法测量C_c与C_obj的相对位置，用R_a, t_a表示。

为了知道C_e与C_obj的相对位置，就必须知道C_e和C_c之间的相对位置，我们用R和t表示该相对位置，由于摄像机是固定在机械手上的，因此一旦固定，R和t必须由标定的方法计算出，因此手眼标定就是要求出R和t。

用A，B，C，D，X表示4*4矩阵，分别描述某两个坐标系的相对位置，如果两个坐标系之间的相对方位由旋转矩阵和平移矢量描述，则:，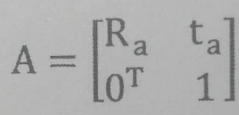

C_obj表示 标定参照物的坐标系，C_c1与C_e1表示 平台运动前的摄像机坐标系与机器人未端执行器坐标系，C_c2与C_e2表示 运动后的这两个坐标系，如果摄像机在C_c1与C_c2两个位置上与C_obj的相对方位用A和B表示 ，在C_c1与C_c2两个位置上可以分别用摄像机标定的方法求出摄像机的内外参数，其中外参即为摄像机在C_c1和C_c2两个位置与C_obj的相对方位，用C表示C_c1与C_c2之间的相对方位，则C=AB^-1，可见在C_c1与C_c2两个位置上分别用标定模板对摄像机进行标定，从而求出A与B，C即为已知矩阵。

再看C_e1与C_e2间的相对方位，由于平台的运动是由机器人控制的，因此运动参数可由机器人的控制器上读出，是已知参数，用矩阵D表示，由于摄像机在运动前后都固定在机器人未端，可见C_c1与C_e1之间的相对方位即为我们所要求的手眼标定参数，我们用X表示，则C_c2与C_e2之间的相对方位也是X。

手眼标定基本方式：

设空间某点P在四个坐标系C_c1，C_c2，C_e1，C_e2的坐标分别为P_c1,P_c2,P_e1，P_e2则有：

P_c1=CP_c2

P_c1=XP_e1

P_e1=DP_e2

P_c2=XP_e2

P_c1=CXP_e2

P_c1=XDP_e2

CX=XD

上面就是手眼标定的基本方程，其物理依据就是机器人未端执行器移动前后，摄像机与其相对位置不变，而X就是要求解 的手眼关系矩阵。

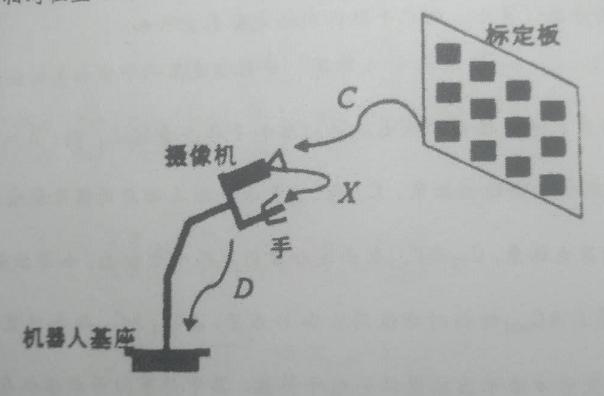
图7.1.9 机器人手眼标定示意图

X是待求参数，正常求出X具有多个解，不能满足实际需要，因此，必须对方程和矩阵赋予一定的几何意义，并充分利用齐次坐标变换矩阵的数学特征，但是仅用一个方程CX=XD仅仅能够获得矩阵X的通解，为了得到方程的唯一解，至少需要两个方程共同确定矩阵中的未知数，C由两次摄像机标定的外参可以得到，D是由实际工作环境中所采用的机器人控制器给出。

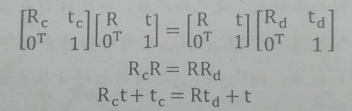
R_c,R_d,t_c,t_d且R，R_c，R_d均为正交单位矩阵，R与t是需要求解的。

关于手眼的理论在很多地方都有阐述，包括R和t的求解，也是有很多方法的，在很多论文地方也可以看到，这里就不一一阐述了。