少有人走的路

如下图所示，cosθ=x/r, 即x=cosθ。

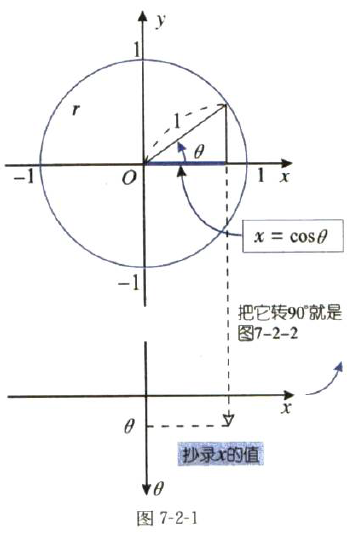
我们习惯把纵轴变成y, 于是函数可以写成y=cosθ。

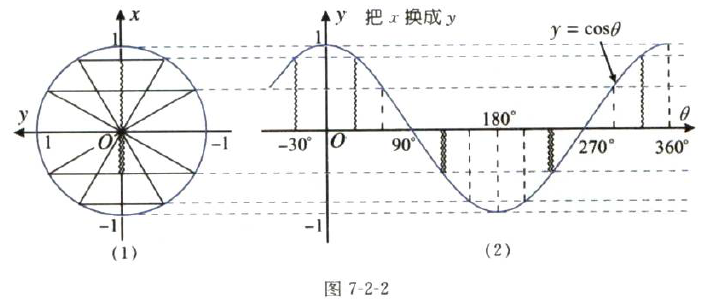
我们把图7-2-2（cosθ）与上一篇的图7-1-3(sinθ)仔细比较一下。（勇哥为了方便大家观察，引用如下）

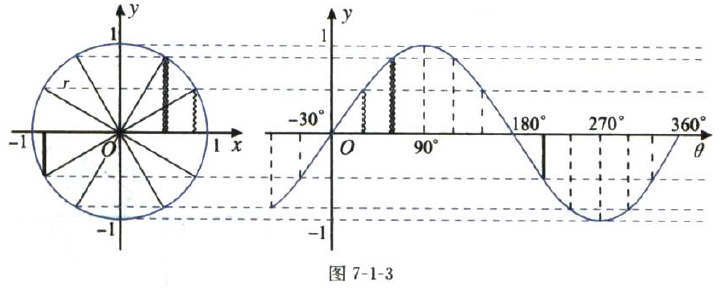
可以看到，cosθ就是sinθ从90°开始的部分。所以这cosθ和sinθ的图象完全一样。

两者的周期都是360°。

我们可以说：

cosθ的图象是sinθ的图象向左平移90°得到的。

也可以反过来说，sinθ的图像是cosθ的图像向右平移90°得到的。

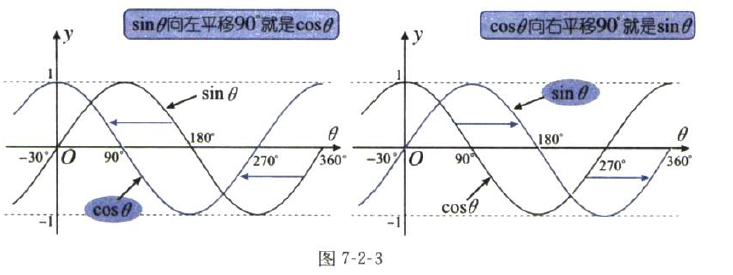
我们也可以引入一个新的名词“相位”，即表示波（图象）的左右的位置。

而sinθ与cosθ的波（图象）的相位相差了90°。

sinθ,cosθ的特点

像sinθ,cosθ那样上下往复运动叫做振动。而从振动中心到最高点（或者到最低点）的距离叫做振幅。

在描述波的时候，周期和振幅往往都是成对出现的（图7-2-4)。

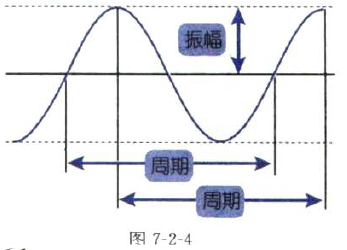
这样，我们就能说出sinθ和cosθ的特点了。

sinθ和cosθ都是周期为360°，振幅为1的周期函数。

振幅为1，通常就写成

-1≤sinθ≤1，-1≤cos≤1θ  

或者用绝值表示： |sinθ|≤1, |cosθ|≤1 

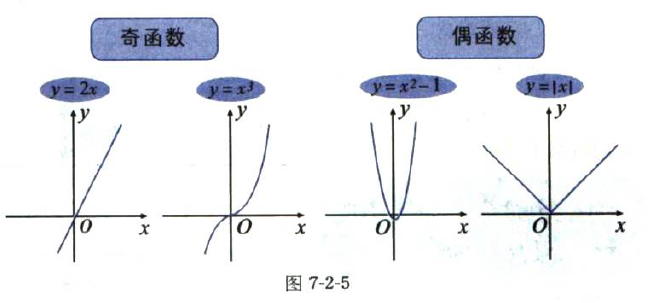
在函数图象中，如果关于原点对称的函数我们叫做奇函数，而图象关于y轴对称的函数叫偶函数。

sinθ的图象关于原点对称,
cosθ的图象关于y轴对称。

举几个例子：

y=2x,y=x³都是奇函数

y=x²-1,y=|x| 都是偶函数

y=xⁿ这个函数中，当n为奇数时，函数就是奇函数，n为偶数时，函数就是偶函数。

下面勇哥用Matlab画上面图7-2-3，如下：

function drawSinCos()

clc
x1=[-30:0.1:360];
y1=sin(degtorad(x1));
plot(x1,y1,'r')
hold on
y2=cos(degtorad(x1));
plot(x1,y2,'b')
xlabel('x(度数)')
ylabel('Y')
legend('sinθ','cosθ')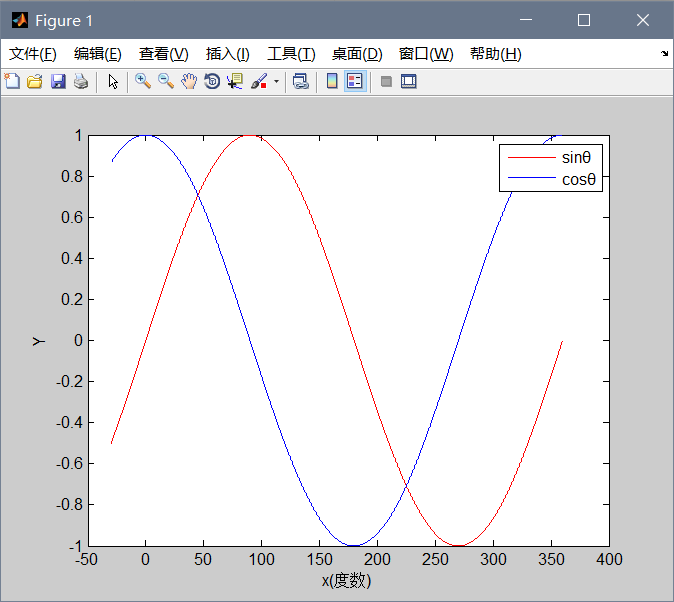

--------------------- 

作者：hackpig

来源：www.skcircle.com

版权声明：本文为博主原创文章，转载请附上博文链接！

本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：