马尔科夫链蒙特卡罗方法(MCMC)解读(二)-行业算法与知识-少有人走的路

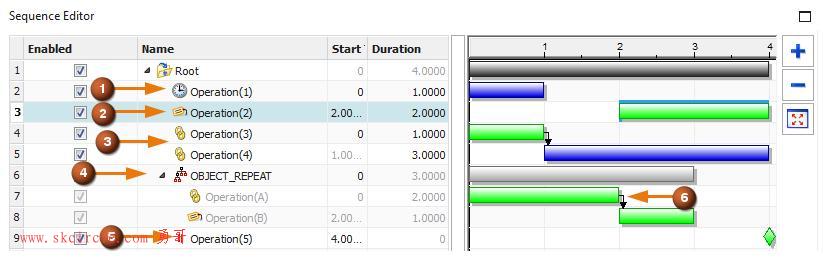
上篇文章的核心思想可以用下图概括：

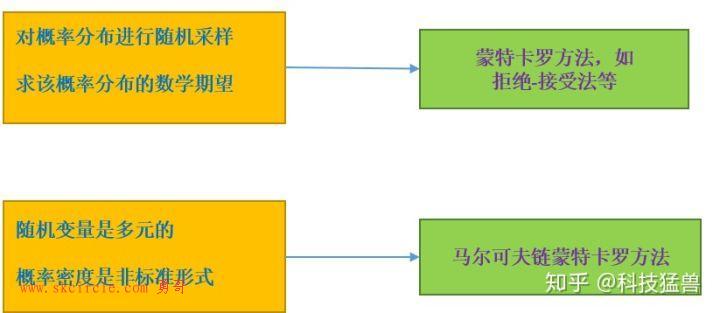
一般的采样问题，以及期望求解，数值近似问题，蒙特卡罗方法都能很好地解决；但遇到多元变量的随机分布以及复杂的概率密度时，仅仅使用蒙特卡罗方法就会显得捉襟见肘，这时就需要这篇文章要讲的马尔可夫链蒙特卡罗法来解决这个问题了。我们先从一维的讲起：

在开始之前首先统一下定义：

我们用符号 $\pi_{i}=\pi(i)=\lim_{t \rightarrow +\infty}{P(X_t=i)}$ 代表一个概率，即马尔科夫链达到平稳分布的时候，状态位于第 $i$ 个状态的概率。

马尔科夫链和蒙特卡罗方法是如何结合在一起的？

一张图解释清楚：

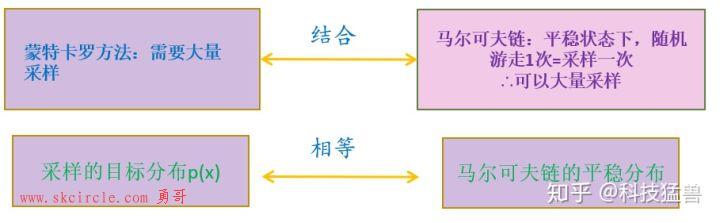
还记得上篇文章中提到的遍历定理吗？如果你忘记了这些定义，请打开上面的链接再复习一遍并点赞：

遍历定理：不可约、非周期且正常返的马尔可夫链，有唯一平稳分布存在，并且转移概率的极限分布是马尔可夫链的平稳分布。

$\lim_{t \rightarrow +\infty }{P(X_t=i|X_0=j)=\pi_i},i=1,2,...;j=1,2,...$

当时让你记了一句话：今后，你如果再遇到某个题目说“一个满足遍历定理的马尔科链，...”你就应该立刻意识到这个马尔科夫链只有一个平稳分布，而且它就是转移概率的极限分布。且随机游走的起始点并不影响得到的结果，即从不同的起始点出发，都会收敛到同一平稳分布。有一个成语叫殊途同归，形容的就是这件事。

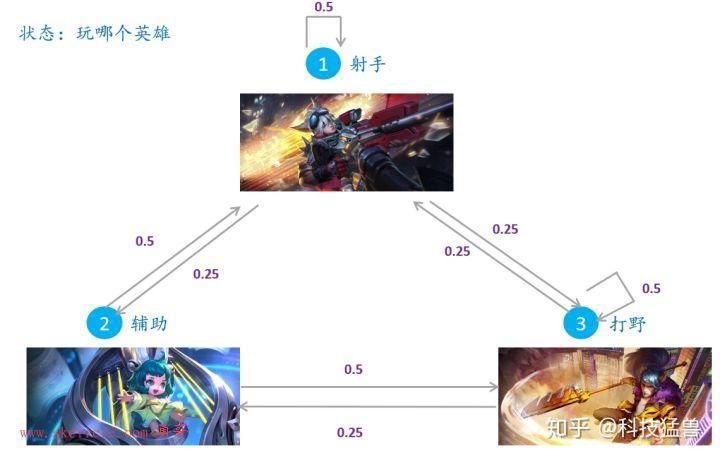
所以，我先定义一个满足遍历定理的马尔可夫链 $X=\left\{ X_0,X_1,...,X_t,... \right\}$ ，每一个状态就代表我在王者荣耀里面玩哪个英雄，比如初始状态 $X_0=1$ 就是玩射手，初始状态 $X_0=3$ 就是玩打野等等。

现在这个马尔科夫链因为满足遍历定理，所以有个平稳分布，代表的就是当 $t\rightarrow +\infty$ 时，我选择哪一个英雄的概率分布。

现在重复一下要解决的问题：1. 从一个目标分布 $p(x)$ 中进行抽样，2. 并求出 $f(x)$ 的数学

期望 $E_{x\sim p(x)}[f(x)]$ ，那我就可以假设：

王者荣耀马尔可夫链的平稳分布=目标分布 $p(x)$

所以，一个惊人的结论诞生了：

在王者荣耀这个马尔科夫链上游走1次，对应的状态就相当于是从目标分布 $p(x)$ 中进行抽样1个样本。换句话说，比如王者荣耀平稳分布是 $[0.5,0.2,0.3]$ ，目标分布 $p(x)$ 也应该是 $[0.5,0.2,0.3]$ ，那在马尔科夫链上游走1次，比如说这把选了辅助，就相当于是在 $p(x)$ 中采样了 $x_2$ 。

所以，每个时刻在这个马尔可夫链上进行随机游走一次，就可以得到一个样本。根据遍历定理，当时间趋于无穷时，样本的分布趋近平稳分布，样本的函数均值趋近函数的数学期望。

所以，当时间足够长时(时刻大于某个正整数 $m$ )，在之后的时间(时刻小于等于某个正整数 $n,n>m$ )里随机游走得到的样本集合 $\left\{ x_{m+1},...,x_{n} \right\}$ 就是目标概率分布的抽样结果，得到的函数均值(遍历均值)就是要计算的数学期望值：

$\hat Ef=\frac{1}{n-m}\sum_{i=m+1}^{n}{f(x_i)}$

到时刻 $m$ 为止的时间段称为燃烧期。

马尔可夫链蒙特卡罗法中得到的样本序列，相邻的样本点是相关的，而不是独立的。因此，在需要独立样本时，可以在该样本序列中再次进行随机抽样，比如每隔一段时间取一次样本，将这样得到的子样本集合作为独立样本集合。马尔可夫链蒙特卡罗法比接受-拒绝法更容易实现，因为只需要定义马尔可夫链，而不需要定义建议分布。一般来说马尔可夫链蒙特卡罗法比接受-拒绝法效率更高，没有大量被拒绝的样本，虽然燃烧期的样本也要抛弃。

最大的问题是：给了我目标分布 $p(x)$ ，对应的王者荣耀马尔可夫链怎么构造？假设收敛的步数为 $m$ ，即迭代了 $m$ 步之后收敛，那 $m$ 是多少？迭代步数 $n$ 又是多少？

常用的马尔可夫链蒙特卡罗法有Metropolis-Hastings算法、吉布斯抽样。

马尔可夫链蒙特卡罗方法的基本步骤是：

构造一个王者荣耀马尔可夫链，使其平稳分布为目标分布 $p(x)$ 。
从某个初始状态 $x_{0}$ 出发，比如第一把选射手，用构造的马尔可夫链随机游走，产生样本序列 $x_{0},x_{1},...,x_{t},...$
应用遍历定理，确定正整数 $m$ 和 $n$ ，得到平稳分布的样本集合： $\left\{ x_{m+1},x_{m+2},...,x_{n}\right\}$ ，求得函数 $f(x)$ 的均值：

$\hat Ef=\frac{1}{n-m}\sum_{i=m+1}^{n}{f(x_i)}$

如何构造一个王者荣耀马尔可夫链？

比如说现在已知的目标分布 $p(x)$ 是 $[0.5,0.2,0.3]$ ，想构造一个马尔可夫链，使它的平稳分布也是 $[0.5,0.2,0.3]$ ，关键还是要求出状态转移矩阵：

$\begin{bmatrix}0.5\\0.2\\0.3\end{bmatrix}=P\begin{bmatrix}0.5\\0.2\\0.3\end{bmatrix}$

在上篇文章中提到过这样一个定理：

定理：满足细致平衡方程的状态分布 $\pi$ 就是该马尔可夫链的平稳分布 $P\pi=\pi$ 。

所以，我只需要找到可以使状态分布 $\pi$ 满足细致平衡方程的矩阵 $P$ 即可，即满足：

$π_iP_{j,i}=π_jP_{i,j}$

仅仅从细致平衡方程还是很难找到合适的矩阵 $P$ 。比如我们的目标平稳分布是 $π$ ,随机找一个马尔科夫链状态转移矩阵 $Q$ ,它是很难满足细致平衡方程，即：

$π_iQ_{j,i}\neπ_jQ_{i,j}$

那么如何使这个等式满足呢？下面我们来看MCMC采样如何解决这个问题。

马尔科夫链蒙特卡罗方法总论

构造一个 $\alpha_{ij}$ 和 $\alpha_{ji}$ ，使上式强制取等号，即：

$π_iQ_{j,i}\alpha_{j,i}=π_jQ_{i,j}\alpha_{i,j}$

要使上式恒成立，只需要取：

$\alpha_{j,i}=π_jQ_{i,j}\\\alpha_{i,j}=π_iQ_{j,i}$

所以，马尔可夫链的状态转移矩阵就呼之欲出了：

$P_{j,i}=Q_{j,i}\alpha_{j,i}\\P_{i,j}=Q_{i,j}\alpha_{i,j}$

咦，状态转移矩阵 $Q$ 是我们胡乱设的， $\alpha$ 值是可以根据 $Q$ 和目标分布 $p(x)$ 算出来的，然后，要构造的满足细致平衡方程的矩阵 $P$ 竟然被我们求出来了！！！

$\alpha_{i,j}$ 的专业术语叫做接受率。取值在 $[0,1]$ 之间，可以理解为一个概率值。

状态转移矩阵 $Q$ 的平稳分布专业术语叫做建议分布(proposal distribution)。

我们回顾一下在一顿数学公式之后，问题的演变过程：

从目标分布 $p(x)$ 中采样

$\rightarrow$ 在马尔科夫链(状态转移矩阵为 $P$ )中随机游走，当达到平稳分布时，每个时刻随机游走一次，就可以得到一个样本。

$\rightarrow$ 在马尔科夫链(状态转移矩阵为 $Q$ )中随机游走，当达到平稳分布时，每个时刻随机游走一次，就可以得到一个样本，这时，以一定的接受率获得，和上篇文章中的拒绝-接受采样极其类似，以一个常见的马尔科夫链状态转移矩阵 $Q$ 通过一定的接受-拒绝概率得到目标转移矩阵 $P$ 。

梳理一下算法：

输入我们任意选定的马尔科夫链状态转移矩阵 $Q$ ，平稳分布 $π$ ，设定状态转移次数阈值 $m$ ，需要的样本个数 $n$ 。
采样一个初始状态 $x_0$ 。
$for\ i\ in\ range(0, n+m):$

从马尔科夫链 $Q$ 中游走一次采样一个样本 $x_*$ 。

产生一个 $[0,1]$ (均匀分布)之间的随机数 $u$ 。

如果 $u<\alpha_{x_*,x_i}=\pi_{x_*}Q_{x_i,x_*}$ (从状态 $x_i$ 到状态 $x_*$ )，则接收转移 $x_i\rightarrow x_*,x_{i+1}=x_*$ 。

否则不接受转移，即 $x_{i+1}=x_i$ 。

样本集 $(x_{m},...,x_{n+m-1})$ 即为我们需要的平稳分布对应的样本集。

Metropolis-Hastings采样算法　　　

MCMC方法帮助我们从目标分布 $p(x)$ 中采样，具体过程为：

从目标分布 $p(x)$ 中采样

$\rightarrow$ 在马尔科夫链(状态转移矩阵为 $P$ )中随机游走，当达到平稳分布时，每个时刻随机游走一次，就可以得到一个样本。

但是问题也会随之而来，即：接受率 $\alpha_{i,j}$ 。取值在 $[0,1]$ 之间，可以理解为一个概率值。这个值通常很小，导致拒绝率太高了，就是说你在马尔科夫链(状态转移矩阵为 $Q$ )中随机游走，刚得到一个样本就被拒绝了，你还得再游走一次，可能这次的又被拒绝了。所以，这样的效率太低，可能我们采样了上百万次马尔可夫链还没有收敛，也就是上面这个 $m$ 要非常非常的大，所以，Metropolis-Hastings采样算法可以解决这个问题：

核心的公式仍然没变：

$π_iQ_{j,i}\alpha_{j,i}=π_jQ_{i,j}\alpha_{i,j}$

只是我让两边的 $\alpha$ 值同时扩大相同的倍数，等式仍然成立，直到其中一侧的 $\alpha$ 值扩大为了1。

假设右边的大一点，原来是：

$π_iQ_{j,i}\times 0.01=π_jQ_{i,j}\times 0.05$

现在是：

$π_iQ_{j,i}\times 0.2=π_jQ_{i,j}\times 1$

这样我们的接受率实际是做了如下改进，即： $\alpha_{j,i}=min\left\{ \frac{π_jQ_{i,j}}{π_iQ_{j,i}},1 \right\}$ 。

现在的算法流程为：

输入我们任意选定的马尔科夫链状态转移矩阵 $Q$ ，平稳分布 $π$ ，设定状态转移次数阈值 $m$ ，需要的样本个数 $n$ 。
采样一个初始状态 $x_0$ 。
$for\ i\ in\ range(0, n+m):$

从马尔科夫链 $Q$ 中游走一次采样一个样本 $x_*$ 。

产生一个 $[0,1]$ (均匀分布)之间的随机数 $u$ 。

如果 $u<\alpha_{x_*,x_i}=min\left\{ \frac{π_{x_{*}}Q_{x_i,x_*}}{π_{x_{i}}Q_{x_*,x_i}},1 \right\}$ (从状态 $x_i$ 到状态 $x_*$ )，则接收转移 $x_i\rightarrow x_*,x_{i+1}=x_*$ 。

否则不接受转移，即 $x_{i+1}=x_i$ 。

样本集 $(x_{m},...,x_{n+m-1})$ 即为我们需要的平稳分布对应的样本集。

计算 $f_{mn}=\frac{1}{n-m}\sum_{i=m+1}^{n}{f(x_i)}$ 。

很多时候，我们选择的马尔科夫链状态转移矩阵如果是对称的，即满足 $Q_{i,j}=Q_{j,i}$ ，这时我们的接受率可以进一步简化为：

$\alpha_{j,i}=min\left\{ \frac{π_j}{π_i},1 \right\}$

M-H采样的Python实现

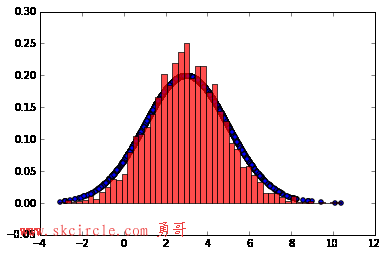
假设目标平稳分布是一个均值10，标准差5的正态分布，而选择的马尔可夫链状态转移矩阵 $Q_{j,i}$ 的条件转移概率是以 $i$ 为均值,方差1的正态分布在位置 $j$ 的值。

import randomimport mathfrom scipy.stats import normimport matplotlib.pyplot as pltdef norm_dist_prob(theta):
    y = norm.pdf(theta, loc=10, scale=5)
    return yT = 5000pi = [0 for i in range(T)]sigma = 1t = 0while t < T-1:
    t = t + 1
    pi_star = norm.rvs(loc=pi[t - 1], scale=sigma, size=1, random_state=None)   #状态转移进行随机抽样
    alpha = min(1, (norm_dist_prob(pi_star[0]) / norm_dist_prob(pi[t - 1])))   #alpha值

    u = random.uniform(0, 1)
    if u < alpha:
        pi[t] = pi_star[0]
    else:
        pi[t] = pi[t - 1]plt.scatter(pi, norm.pdf(pi, loc=10, scale=5),label='Target Distribution', c= 'red')num_bins = 50plt.hist(pi, num_bins, density=1, facecolor='green', alpha=0.7,label='Samples Distribution')plt.legend()plt.show()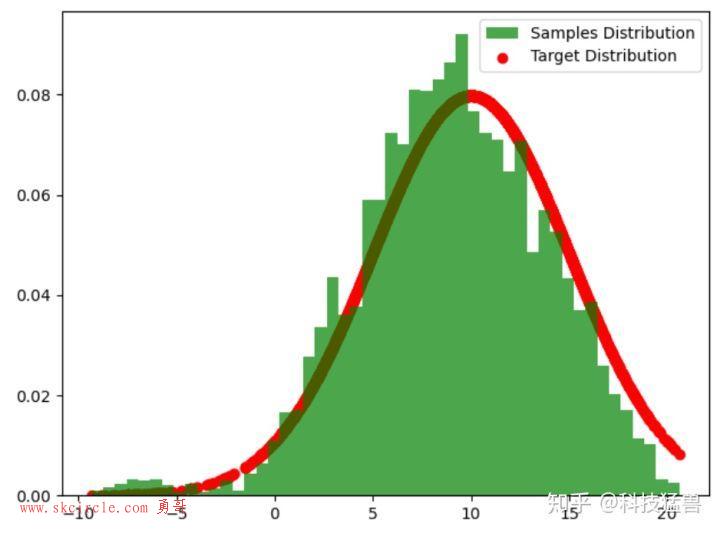

再假设目标平稳分布是一个 $a=2.37,b=0.627$ 的 $\beta$ 分布，而选择的马尔可夫链状态转移矩阵 $Q_{j,i}$ 的条件转移概率是以 $i$ 为均值,方差1的正态分布在位置 $j$ 的值。

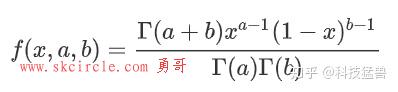
import randomimport mathfrom scipy.stats import betafrom scipy.stats import normimport matplotlib.pyplot as plta, b = 2.31, 0.627def norm_dist_prob(theta):
    y = beta(2.31, 0.627).pdf(theta)
    return yT = 5000pi = [0 for i in range(T)]sigma = 1t = 0while t < T-1:
    t = t + 1
    pi_star = norm.rvs(loc=pi[t - 1], scale=sigma, size=1, random_state=None)   #状态转移进行随机抽样
    alpha = min(1, (norm_dist_prob(pi_star[0]) / norm_dist_prob(pi[t - 1])))   #alpha值

    u = random.uniform(0, 1)
    if u < alpha:
        pi[t] = pi_star[0]
    else:
        pi[t] = pi[t - 1]plt.scatter(pi, beta(2.31, 0.627).pdf(pi),label='Target Distribution', c= 'red')num_bins = 50plt.hist(pi, num_bins, density=1, facecolor='green', alpha=0.7,label='Samples Distribution')plt.legend()plt.show()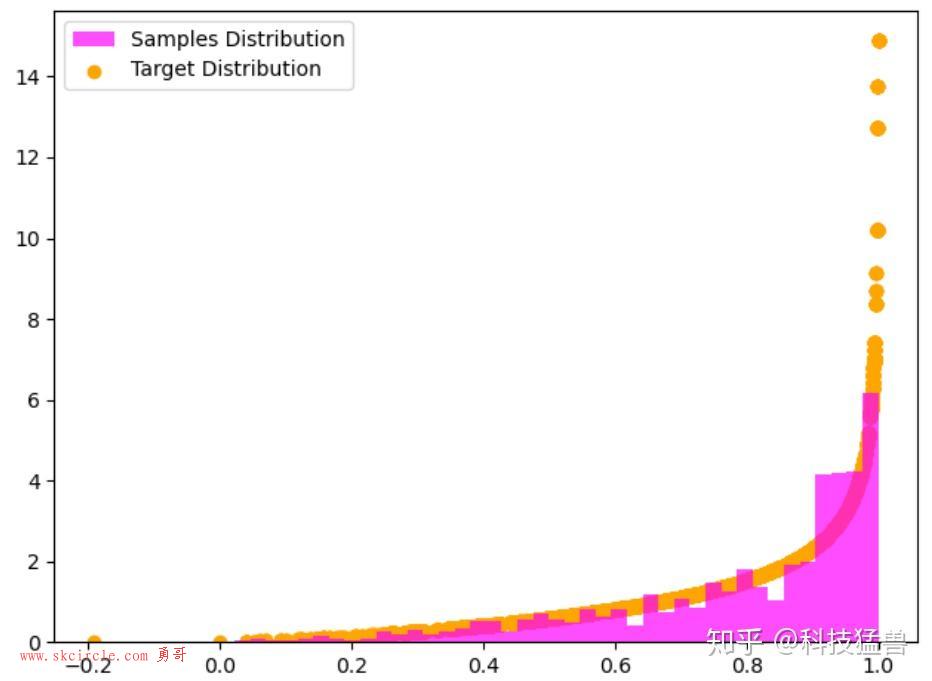

输出的图中可以看到采样值的分布与真实的分布之间的关系如下，采样集还是比较拟合对应分布的。

吉布斯抽样

M-H采样由于接受率计算式 $min\{\frac{\pi(j)Q(j,i)}{\pi(i)Q(i,j)},1\}$ 的存在，在高维时需要的计算时间非常的可观，算法效率仍然很低。而且，很多时候我们甚至很难求出目标的各特

征维度联合分布，但是可以方便求出各个特征之间的条件概率分布。所以我们希望对条件概率

分布进行抽样，得到样本的序列。

用大白话说，吉布斯抽样解决的问题和M-H方法解决的问题是一致的，都是从给定一个已知的目标分布 $p(x)$ 中进行采样，并估计某个函数的期望值，区别只不过是此时， $p(x)$ 是一个多维的随机分布， $p(x)$ 的联合分布复杂，难以采样，但条件分布较容易，这样吉布斯抽样效果更好。

其基本做法是，从联合概率分布定义条件概率分布，依次对条件概率分布进行抽样，得到样本的序列。可以证明这样的抽样过程是在一个马尔可夫链上的随机游走，每一个样本对应着马尔可夫链的状态，平稳分布就是目标的联合分布。整体成为一个马尔可夫链蒙特卡罗法，燃烧期之后的样本就是联合分布的随机样本。

假设多元变量的联合概率分布为 $p(x)=p(x_1,x_2,...,x_k)$ ，吉布斯采样从一个初始样本

$x^{(0)}=(x_1^{(0)},x_2^{(0)},...,x_k^{(0)})^T$ 出发，不断进行迭代，每一次迭代得到联合分布

$x^{(i)}=(x_1^{(i)},x_2^{(i)},...,x_k^{(i)})^T$ 。最终得到样本序列 $x_1,x_2,...,x_k$ 。

首先讨论二维的数据分布：

重复一下细致平衡方程， $π_iP_{j,i}=π_jP_{i,j}$ ，或者写成 $π(i)P(j,i)=π(j)P(i,j)$ 。

在数据分布是二维的时候， $\pi(x_1,x_2)$ 就变成了二维联合概率分布，目标分布

$p(x)=p(x_1,x_2)$ ，而且我们希望 $\pi(x_1,x_2)=p(x_1,x_2)$ 。

首先我们可以把二维联合概率分布的条件分布给求出来：

$\pi(x_1|x_2)=\frac{\pi(x_1,x_2)}{\int\pi(x_1,x_2)dx_1},\pi(x_2|x_1)=\frac{\pi(x_1,x_2)}{\int\pi(x_1,x_2)dx_2}$

所以，我们现在不但有了目标分布(联合分布)，还有目标分布(条件分布)。

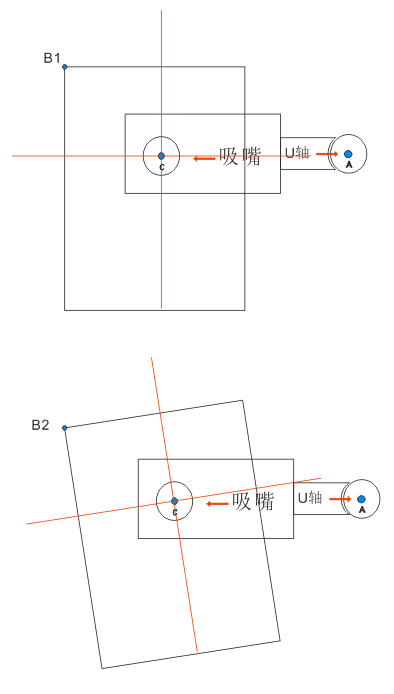
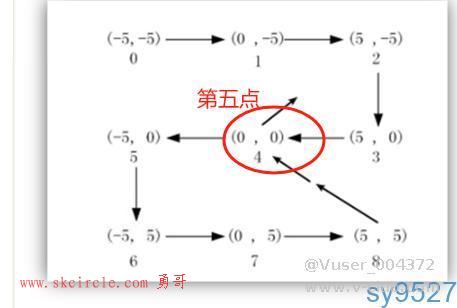
接下来问题还是从二维分布 $p(x)$ 上进行采样，接下来这3个图代表状态转移的过程：

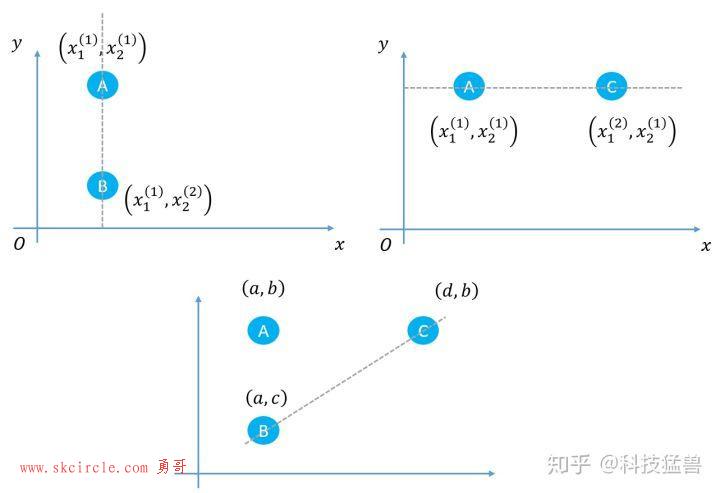
如下图所示为二维的状态空间，ABC代表3个不同的状态。

对于第1个图：

$\pi(x_{1}^{(1)},x_{2}^{(1)})\pi(x_{2}^{(2)}|x_{1}^{(1)})=\pi(x_{1}^{(1)})\pi(x_{2}^{(1)}|x_{1}^{(1)})\pi(x_{2}^{(2)}|x_{1}^{(1)})$

$\pi(x_{1}^{(1)},x_{2}^{(2)})\pi(x_{2}^{(1)}|x_{1}^{(1)})=\pi(x_{1}^{(1)})\pi(x_{2}^{(2)}|x_{1}^{(1)})\pi(x_{2}^{(1)}|x_{1}^{(1)})$

发现上面2个式子右端是一样的。所以：

$\pi(x_{1}^{(1)},x_{2}^{(1)})\pi(x_{2}^{(2)}|x_{1}^{(1)})=\pi(x_{1}^{(1)},x_{2}^{(2)})\pi(x_{2}^{(1)}|x_{1}^{(1)})$

可以写成：

$\pi(A)\pi(x_{2}^{(2)}|x_{1}^{(1)})=\pi(B)\pi(x_{2}^{(1)}|x_{1}^{(1)})$

这个式子好像和细致平衡方程有点像，此时A和B是在一条直线： $x_1=x_{1}^{(1)}$ 上的。A点在上方，B点在下方，可以看做是一维分布，所以上式可以看作是：

$\pi(上)\pi(上\rightarrow下)=\pi(下)\pi(下\rightarrow上)$

就是细致平衡方程，所以 $\pi(x_{2}|x_{1}^{(1)})$ 就是我们要找的马尔科夫链的状态转移概率。

对于第2个图：

$\pi(x_{1}^{(1)},x_{2}^{(1)})\pi(x_{1}^{(2)}|x_{2}^{(1)})=\pi(x_{2}^{(1)})\pi(x_{1}^{(1)}|x_{2}^{(1)})\pi(x_{1}^{(2)}|x_{2}^{(1)})$

$\pi(x_{1}^{(2)},x_{2}^{(1)})\pi(x_{1}^{(1)}|x_{2}^{(1)})=\pi(x_{2}^{(1)})\pi(x_{1}^{(2)}|x_{2}^{(1)})\pi(x_{1}^{(1)}|x_{2}^{(1)})$

发现上面2个式子右端是一样的。所以：

$\pi(x_{1}^{(1)},x_{2}^{(1)})\pi(x_{1}^{(2)}|x_{2}^{(1)})=\pi(x_{1}^{(2)},x_{2}^{(1)})\pi(x_{1}^{(1)}|x_{2}^{(1)})$

可以写成：

$\pi(A)\pi(x_{1}^{(2)}|x_{2}^{(1)})=\pi(C)\pi(x_{1}^{(1)}|x_{2}^{(1)})$

这个式子好像和细致平衡方程有点像，此时A和C是在一条直线： $x_2=x_{2}^{(1)}$ 上的。A点在左侧，B点在右侧，可以看做是一维分布，所以上式可以看作是：

$\pi(左)\pi(左\rightarrow右)=\pi(右)\pi(右\rightarrow左)$

就是细致平衡方程，所以 $\pi(x_{1}|x_{2}^{(1)})$ 就是我们要找的马尔科夫链的状态转移概率。

对于第3个图：

把上2图的结论整合在一起可以得到最终的结论：

$\pi(左下)\pi(左下\rightarrow右上)=\pi(右上)\pi(右上\rightarrow左下)$

就是细致平衡方程，也就是说，我们在不同的维度上分别将 $\pi(x_{2}|x_{1}^{(1)})$ 和 $\pi(x_{1}|x_{2}^{(1)})$ 作为马尔科夫链的状态转移概率，就能实现最终的效果，即：马尔科夫链达到平稳后的一次随机游走等同于高维分布的一次采样。这就是Gibbs采样。

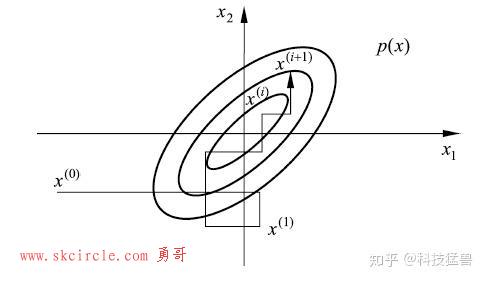
二维Gibbs采样的算法流程为：

输入平稳分布 $π(x_1,x_2)$ ，设定状态转移次数阈值 $m$ ，需要的样本个数 $n$ 。
采样一个初始状态 $x_1^{(0)},x_2^{(0)}$ 。
$for\ i\ in\ range(0, n+m):$

从条件概率分布 $P(x_{2}|x_{1}^{(t)})$ 中采样得到样本 $x_{2}^{(t+1)}$ 。

从条件概率分布 $P(x_{1}|x_{2}^{(t+1)})$ 中采样得到样本 $x_{1}^{(t+1)}$ 。

样本集 $\left\{ (x_{1}^{m+1},x_{2}^{m+1}) ,(x_{1}^{m+2},x_{2}^{m+2}),...,(x_{1}^{m+n},x_{2}^{m+n})\right\}$ 即为我们需要的平稳分布对应的样本集。

计算 $f_{mn}=\frac{1}{n-m}\sum_{i=m+1}^{n}{f(x_i)}$ 。

所以采样过程为：

$(x_1^{(1)},x_2^{(1)})\rightarrow(x_1^{(1)},x_2^{(2)})\rightarrow(x_1^{(2)},x_2^{(2)})...\rightarrow(x_1^{(n+m)},x_2^{(n+m)})$

采样是在两个坐标轴上不停的轮换的。

同理可得，多维Gibbs采样的算法流程为：

输入平稳分布 $π(x_1,x_2,...,x_n)$ ，设定状态转移次数阈值 $m$ ，需要的样本个数 $n$ 。
采样一个初始状态 $x_1^{(0)},x_2^{(0)},...,x_n^{(0)}$ 。
$for\ i\ in\ range(0, n+m):$

从条件概率分布 $P(x_{1}|x_{2}^{(t)},x_{3}^{(t)},...,x_{n}^{(t)})$ 中采样得到样本 $x_{1}^{(t+1)}$ 。

从条件概率分布 $P(x_{2}|x_{1}^{(t+1)},x_{2}^{(t)},...,x_{n}^{(t)})$ 中采样得到样本 $x_{2}^{(t+1)}$ 。

从条件概率分布 $P(x_{j}|x_{1}^{(t+1)},x_{2}^{(t+1)},...,x_{j-1}^{(t+1)},x_{j+1}^{(t)},...x_{n}^{(t)})$ 中采样得到样本 $x_{j}^{(t+1)}$ 。

样本集 $\left\{ (x_{1}^{m+1},x_{2}^{m+1}) ,(x_{1}^{m+2},x_{2}^{m+2}),...,(x_{1}^{m+n},x_{2}^{m+n})\right\}$ 即为我们需要的平稳分布对应的样本集。

计算 $f_{mn}=\frac{1}{n-m}\sum_{i=m+1}^{n}{f(x_i)}$ 。

二维Gibbs采样实例python实现

假设我们要采样的是一个二维正态分布 $N(\mu,\Sigma)$ ，其中： $\mu=(\mu_{1},\mu_{2})=(5,-1)$ ， $\Sigma=\begin{pmatrix}\sigma_{1}^{2} &\rho \sigma_{1}\sigma_{2} \\ \rho \sigma_{1}\sigma_{2} & \sigma_{2}^{2}\end{pmatrix}=\begin{pmatrix}1 &1 \\ 1 & 4\end{pmatrix}$ ;

首先需要求得：采样过程中的需要的状态转移条件分布：

$P(x_{1}|x_{2})=N\left(\mu_{1}+\rho \sigma_{1}/\sigma_{2}(x_{2}-\mu_{2}),(1-\rho^{2})\sigma_{1}^{2}\right)\\$

$P(x_{2}|x_{1})=N\left(\mu_{2}+\rho \sigma_{2}/\sigma_{1}(x_{1}-\mu_{1}),(1-\rho^{2})\sigma_{2}^{2}\right)\\$

证：

$f(x_1,x_2)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}exp\left\{ -\frac{1}{2(1-\rho^2)}\left[ (\frac{x_1-\mu_1}{\sigma_1})^2-2r(\frac{x_1-\mu_1}{\sigma_1})(\frac{x_2-\mu_2}{\sigma_2})+(\frac{x_2-\mu_2}{\sigma_2})^2 \right] \right\}$

$f(x_2)=\frac{1}{\sqrt{2\pi}\sigma_2}exp\left\{ -\frac{(x-\mu_2)^2}{2\sigma_2^2} \right\}$

所以：

$f(x_1|x_2)=\frac{1}{\sqrt{2\pi}\sigma_1\sqrt{1-\rho^2}}exp\left\{ -\frac{1}{2(1-\rho^2)\sigma_1^2}\left[ x_1-\mu_1-\frac{\sigma_1}{\sigma_2}\rho(x_2-\mu_2)\right]^2 \right\}$

得证。

import randomimport mathfrom scipy.stats import betafrom scipy.stats import normimport matplotlib.pyplot as pltfrom mpl_toolkits.mplot3d import Axes3Dfrom scipy.stats import multivariate_normalsamplesource = multivariate_normal(mean=[5,-1], cov=[[1,0.5],[0.5,2]])def p_ygivenx(x, m1, m2, s1, s2):
    return (random.normalvariate(m2 + rho * s2 / s1 * (x - m1), math.sqrt(1 - rho ** 2) * s2))def p_xgiveny(y, m1, m2, s1, s2):
    return (random.normalvariate(m1 + rho * s1 / s2 * (y - m2), math.sqrt(1 - rho ** 2) * s1))N = 5000K = 20x_res = []y_res = []z_res = []m1 = 5m2 = -1s1 = 1s2 = 2rho = 0.5y = m2for i in range(N):
    for j in range(K):
        x = p_xgiveny(y, m1, m2, s1, s2)   #y给定得到x的采样
        y = p_ygivenx(x, m1, m2, s1, s2)   #x给定得到y的采样
        z = samplesource.pdf([x,y])
        x_res.append(x)
        y_res.append(y)
        z_res.append(z)num_bins = 50plt.scatter(x_res, norm.pdf(x_res, loc=5, scale=1),label='Target Distribution x', c= 'green')plt.scatter(y_res, norm.pdf(y_res, loc=-1, scale=2),label='Target Distribution y', c= 'orange')plt.hist(x_res, num_bins, density=1, facecolor='Cyan', alpha=0.5,label='x')plt.hist(y_res, num_bins, density=1, facecolor='magenta', alpha=0.5,label='y')plt.title('Histogram')plt.legend()plt.show()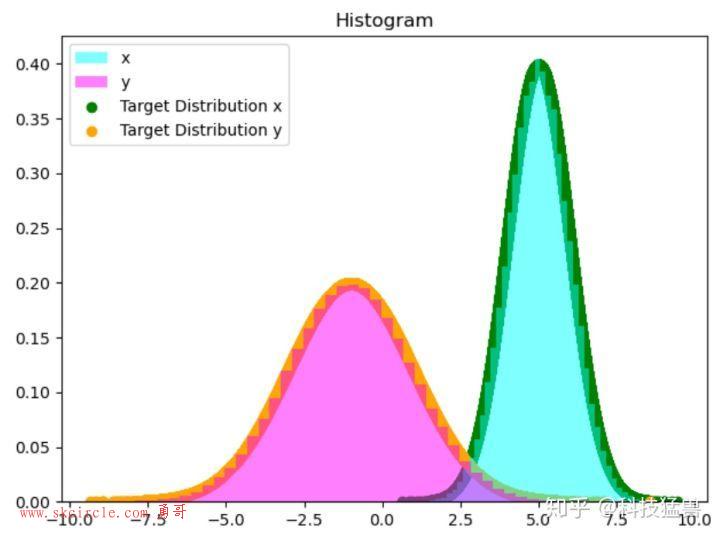

然后我们看看样本集生成的二维正态分布，代码如下：

fig = plt.figure()ax = Axes3D(fig, rect=[0, 0, 1, 1], elev=30, azim=20)ax.scatter(x_res, y_res, z_res,marker='o',c= '#00CED1')plt.show()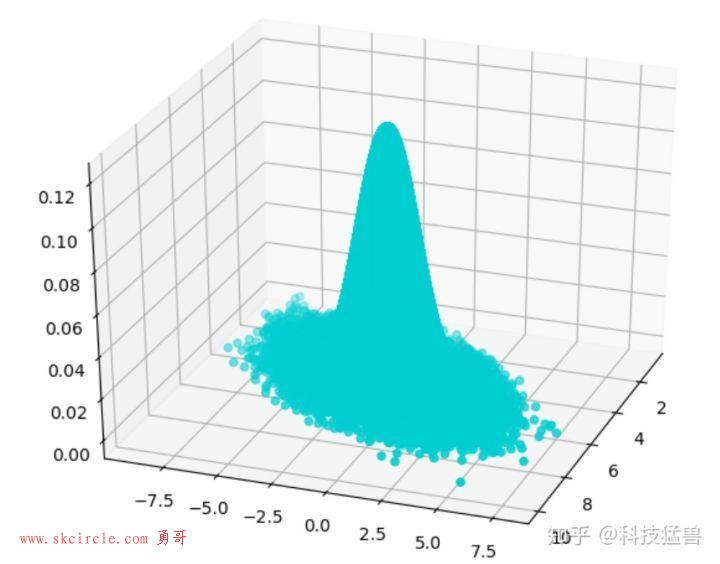

MCMC算法的一般流程是：先给定目标分布完成采样过程，若目标分布是一维的，就用M-H采样方法；若目标分布是多维的，就用Gibbs采样方法。采样结束之后，蒙特卡罗方法来用样本集模拟求和，求出目标变量(期望等)的统计值作为估计值。这套思路被应用于概率分布的估计、定积分的近似计算、最优化问题的近似求解等问题，特别是被应用于统计学习中概率模型的学习与推理，是重要的统计学习计算方法。

参考：

MCMC(三)MCMC采样和M-H采样 - 刘建平Pinard - 博客园www.cnblogs.com

本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：

一	二	三	四	五	六	日
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30

少有人走的路

2020-11-13 10:18:00