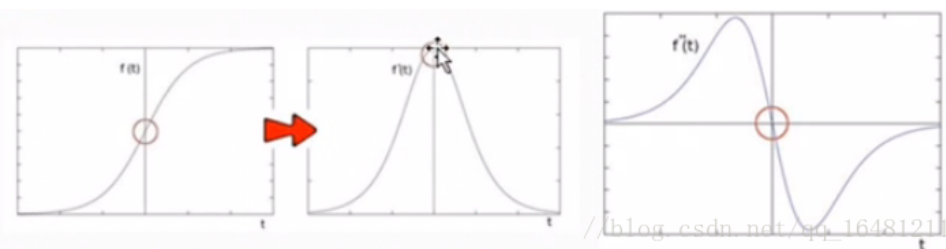
少有人走的路理论：
在二阶微分的时候，最大变化处的值为零即边缘是零值，通过二阶导数计算，依据理论我们可以计算出图像二阶导数，提取边缘。
处理流程：
高斯模糊-去噪声GaussianBlur()
转化为灰度图像cvtColor()
拉普拉斯-二阶导数计算Laplacian()
提取绝对值convertScaleAbs()
显示结果
代码：
#include <opencv2/opencv.hpp>
#include <iostream>
#include <math.h>
using namespace cv;
int main(int argc,char ** argv)
{
Mat src,gray_src,edge_img,dst;
src = imread("1.jpg");
namedWindow("input window",CV_WINDOW_AUTOSIZE);
imshow("input window",src);
GaussianBlur(src,dst,Size(3,3),0,0);
cvtColor(dst,gray_src,CV_BGR2GRAY);
Laplacian(gray_src,edge_img,CV_16S,3);
convertScaleAbs(edge_img,edge_img);
imshow("1",edge_img);
waitKey(0);
return 0;
}效果：
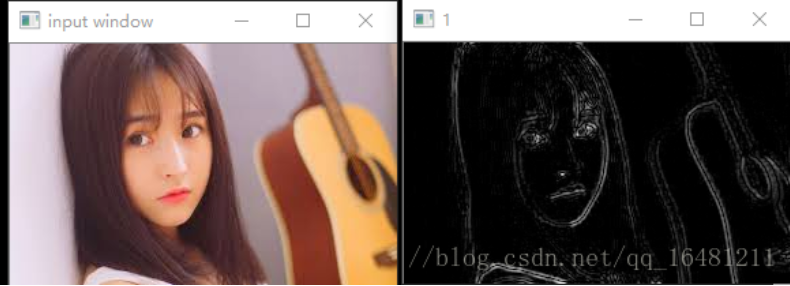
github源码和图片下载地址：
https://github.com/MRwangmaomao/OpencvTestLaplace-Project.git
本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：
