在二维平面上,常用的有以下三种基本的图形变化:
1)Translation
2)Scale
3)Rotation
在Android的开发中,我们也经常会用到这样的一些图形变换,尤其是我们在写自定义View时,更是会经常利用到Matrix来实现一些效果,比如平移,旋转,缩放及切变等,相信很多朋友应该很想知道,矩阵实现这种变换的原理是什么,什么是矩阵的左乘右乘,它们在实现效果上有什么差别吗?今天就让我们一起来看一下吧。
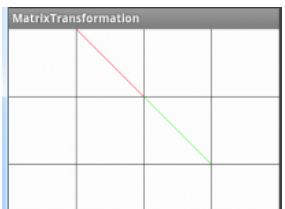
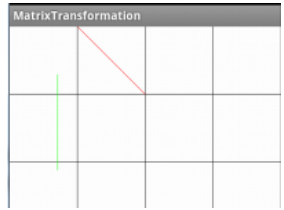
都是由点组成的
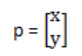
而下面这条红色的直线则是由一组组的点组成的,起始点是(120,0),终点是(240,120)。

Translation(平移)
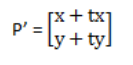
这样的一个变换translation也可以用一对值来表示,t = {tx, ty},其中tx是在x坐标上的偏移量,而ty是在y坐标上的偏移量。移动点 p 到 p',我们只要加上这个偏移就行,如果用矩阵或者向量来表示就是:
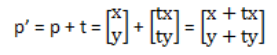
Scale(缩放)
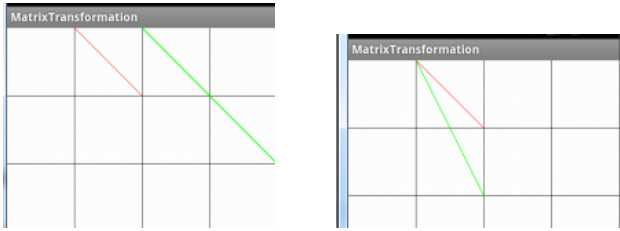
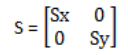
那么缩放后的直线的点就是:
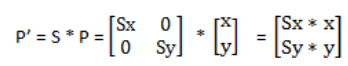
Rotation(旋转)
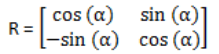
同样的,旋转后的点就是根据下面的矩阵相乘而得出来的结果:
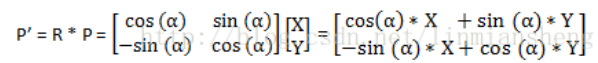
Combine Transformation (组合变换)
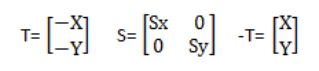
那么它应该实施的变换就如下:先平移 T 到原点,再基于原点进行缩放(或者旋转),然后再平移回去,
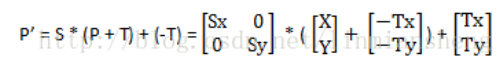
其实这一步,我们可以在Canvas的代码中看到的,如下:
/**
* Preconcat the current matrix with the specified scale.
*
* @param sx The amount to scale in X
* @param sy The amount to scale in Y
* @param px The x-coord for the pivot point (unchanged by the scale)
* @param py The y-coord for the pivot point (unchanged by the scale)
*/
public final void scale(float sx, float sy, float px, float py) {
translate(px, py);
scale(sx, sy);
translate(-px, -py);
}上面代码中的轴点的实现,其实就是对于平移的来回操作,至于为什么是translate(px,py)在前,而translate(-px,py)在后呢,这涉及到矩阵左乘和右乘的计算,后面我们会谈到的。
Homogeneous Coordinates(齐次坐标)
在上面的矩阵中,我们可以看到平移的矩阵是相加的,而旋转跟缩放的矩阵都是相乘的,这样计算起来多麻烦呀!于是为了方便计算,大家都统一用一种方式来进行计算,聪明的计算机图形科学家,它们就设计出这样一种坐标系,叫homogeneous coordinates,而它的目的只是为了更加方便地去用矩阵来计算图形的变换,没有其他。
那什么是齐次坐标呢?
其实就是在原来2D的维度,再加上一个新的维度,多出来的维度的值永远是1,比如点的矩阵就变成:

————————————————
版权声明:本文为CSDN博主「linmiansheng」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/linmiansheng/article/details/18801947

 少有人走的路
少有人走的路