最近在项目中要进行图像的特征提取工作,为了便于以后查阅和使用,遂写博客以记录。
说到图像的纹理特征,大家能想到的就是灰度共生矩阵(Gray-Level Co-Occurrence Matrix, GLCM)、灰度游程矩阵(Gray-Level Run-Length Matrix, GLRLM)、局部二值模式(Local Binary Pattern, LBP)和方向梯度直方图(Histogram of Oriented Gradient, HOG)。
这篇博文主要总结一下灰度游程矩阵,顾名思义,灰度游程矩阵就是灰度值游行的长度所组成的矩阵。我们直接上定义,记灰度共生矩阵为D[i, j, theta],其中i表示原始图像中的像素值,i的所有取值为原始图像的灰度级数,j表示像素值所游走的长度,也就是在图像中有j个连续的i出现,theta表示计算的方向,一般有0度、45度、90度和135度。
下面以一个例子说明:
Img = [[1, 1, 0, 0], [1, 1, 0, 0], [0, 0, 2, 2], [0, 0, 2, 2]]
我们以theta=0计算GLRLM,theta=0也就是按照水平方向计算,按照上述可以将灰度游程矩阵表示为D[i, j, theta],D.shape=(3, 4, 1),其中3表示灰度阶数[0, 1, 2];4表示最长的数据值,即对角线长为4;1表示theta的个数,即只有theta=0。按照水平方向计算,统计像素0,0连续出现4次为0, 0连续出现3次为0,0连续出现2次为4,0连续出现1次为0(这里需要注意:因为在计算0连续出现2次时已经计算了所有的0,所以再计算0出现一次时就不将刚才计算过的0列入其中),所以像素0结果为[0, 4, 0, 0]。按照以上方法计算像素1结果为[0, 2, 0, 0],所以有:
按照theta=0度计算结果: P_0 = [[0, 4, 0, 0], [0, 2, 0, 0], [0, 2, 0, 0]]按照theta=45度计算结果: P_45 = [[4, 0, 0, 1], [2, 1, 0, 0], [2, 1, 0, 0]]按照theta=90度计算结果: P_90 = [[0, 4, 0, 0], [0, 2, 0, 0], [0, 2, 0, 0]]按照theta=135度计算结果: P_135 = [[4, 2, 0, 0], [2, 1, 0, 0], [2, 1, 0, 0]]
此处要注意两点:
每次计算时从最长的像素串开始统计;
对于已经统计过的像素串,在计算比其长度小的子串时应该舍弃。
说清楚了计算方法,我们接下来上代码:
def getGrayLevelRumatrix(self, array, theta): ''' 计算给定图像的灰度游程矩阵 参数: array: 输入,需要计算的图像 theta: 输入,计算灰度游程矩阵时采用的角度,list类型,可包含字段:['deg0', 'deg45', 'deg90', 'deg135'] glrlm: 输出,灰度游程矩阵的计算结果 ''' P = array x, y = P.shape min_pixels = np.min(P) # 图像中最小的像素值 run_length = max(x, y) # 像素的最大游行长度 num_level = np.max(P) - np.min(P) + 1 # 图像的灰度级数 deg0 = [val.tolist() for sublist in np.vsplit(P, x) for val in sublist] # 0度矩阵统计 deg90 = [val.tolist() for sublist in np.split(np.transpose(P), y) for val in sublist] # 90度矩阵统计 diags = [P[::-1, :].diagonal(i) for i in range(-P.shape[0]+1, P.shape[1])] #45度矩阵统计 deg45 = [n.tolist() for n in diags] Pt = np.rot90(P, 3) # 135度矩阵统计 diags = [Pt[::-1, :].diagonal(i) for i in range(-Pt.shape[0]+1, Pt.shape[1])] deg135 = [n.tolist() for n in diags] def length(l): if hasattr(l, '__len__'): return np.size(l) else: i = 0 for _ in l: i += 1 return i glrlm = np.zeros((num_level, run_length, len(theta))) # 按照统计矩阵记录所有的数据, 第三维度表示计算角度 for angle in theta: for splitvec in range(0, len(eval(angle))): flattened = eval(angle)[splitvec] answer = [] for key, iter in groupby(flattened): # 计算单个矩阵的像素统计信息 answer.append((key, length(iter))) for ansIndex in range(0, len(answer)): glrlm[int(answer[ansIndex][0]-min_pixels), int(answer[ansIndex][1]-1), theta.index(angle)] += 1 # 每次将统计像素值减去最小值就可以填入GLRLM矩阵中 return glrlm
做简单说明,每次计算时按照需要计算的角度将矩阵进行整理然后统计,填入初始化的GLRLM矩阵中。计算0度,直接对原始图像按行整理,然后使用groupby()函数对每行的数进行统计,例如[0, 0, 2, 3, 3, 4, 6],groupby的结果为[(0, 2), (2, 1), (3, 2), (4, 1), (6, 1)],圆括号内的第一个数代表真实的像素值,第二个值代表像素值出现的次数,计算90度时只需将原始矩阵转置,然后采用同样方法统计。计算135度,对于一个矩阵,采用diagonal()函数取对角线,采用加位移参数的方式取遍所有135度值,使用groupby()完成统计,计算45度时只需将原始矩阵顺时针旋转270度,同样采用取对角线方式计算即可。
灰度游程矩阵只是对图像像素信息的度量和统计,在实际使用的过程中还需要针对生成的灰度游程矩阵进行计算,得到基于灰度共生矩阵的图像特征信息。下面代码实现了对11个灰度游程矩阵特征的提取:
在实际代码之前先写几个公用的函数,完成下标i和j的计算(calcuteIJ())、按照指定维度进行乘除操作(apply_over_degree())和计算所有像素和(calcuteS()),如下:
def apply_over_degree(function, x1, x2): rows, cols, nums = x1.shape result = np.ndarray((rows, cols, nums)) for i in range(nums): print(x1[:, :, i]) result[:, :, i] = function(x1[:, :, i], x2) print(result[:, :, i]) result[result == np.inf] = 0 result[np.isnan(result)] = 0 return result def calcuteIJ(rlmatrix): gray_level, run_length, _ = rlmatrix.shape I, J = np.ogrid[0:gray_level, 0:run_length] return I, J+1 def calcuteS(rlmatrix): return np.apply_over_axes(np.sum, rlmatrix, axes=(0, 1))[0, 0]
1. Short Run Emphasis(SRE)
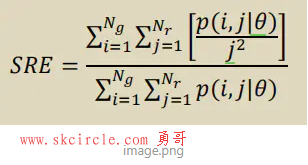
def getShortRunEmphasis(rlmatrix): I, J = self.calcuteIJ(rlmatrix) numerator = np.apply_over_axes(np.sum, self.apply_over_degree(np.divide, rlmatrix, (J*J)), axes=(0, 1))[0, 0] S = self.calcuteS(rlmatrix) return numerator / S
2. Long Run Emphasis(LRE)
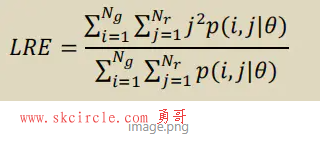
def getLongRunEmphasis(rlmatrix): I, J = self.calcuteIJ(rlmatrix) numerator = np.apply_over_axes(np.sum, self.apply_over_degree(np.multiply, rlmatrix, (J*J)), axes=(0, 1))[0, 0] S = self.calcuteS(rlmatrix) return numerator / S
3. Gray Level Non-Uniformity(GLN)
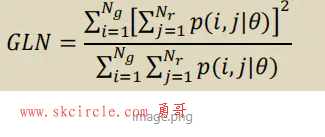
def getGrayLevelNonUniformity(rlmatrix): G = np.apply_over_axes(np.sum, rlmatrix, axes=1) numerator = np.apply_over_axes(np.sum, (G*G), axes=(0, 1))[0, 0] S = self.calcuteS(rlmatrix) return numerator / S
以下同上述一样,就不具体列出来了

# 4. RLN
def getRunLengthNonUniformity(rlmatrix):
R = np.apply_over_axes(np.sum, rlmatrix, axes=0)
numerator = np.apply_over_axes(np.sum, (R*R), axes=(0, 1))[0, 0]
S = self.calcuteS(rlmatrix)
return numerator / S # 5. RP
def getRunPercentage(rlmatrix):
gray_level, run_length, _ = rlmatrix.shape
num_voxels = gray_level * run_length return self.calcuteS(rlmatrix) / num_voxels # 6. LGLRE
def getLowGrayLevelRunEmphasis(rlmatrix):
I, J = self.calcuteIJ(rlmatrix)
numerator = np.apply_over_axes(np.sum, self.apply_over_degree(np.divide, rlmatrix, (I*I)), axes=(0, 1))[0, 0]
S = self.calcuteS(rlmatrix)
return numerator / S # 7. HGLRE
def getHighGrayLevelRunEmphais(rlmatrix):
I, J = self.calcuteIJ(rlmatrix)
numerator = np.apply_over_axes(np.sum, self.apply_over_degree(np.multiply, rlmatrix, (I*I)), axes=(0, 1))[0, 0]
S = self.calcuteS(rlmatrix)
return numerator / S # 8. SRLGLE
def getShortRunLowGrayLevelEmphasis(rlmatrix):
I, J = self.calcuteIJ(rlmatrix)
numerator = np.apply_over_axes(np.sum, self.apply_over_degree(np.divide, rlmatrix, (I*I*J*J)), axes=(0, 1))[0, 0]
S = self.calcuteS(rlmatrix)
return numerator / S # 9. SRHGLE
def getShortRunHighGrayLevelEmphasis(rlmatrix):
I, J = self.calcuteIJ(rlmatrix)
temp = self.apply_over_degree(np.multiply, rlmatrix, (I*I))
print('-----------------------')
numerator = np.apply_over_axes(np.sum, self.apply_over_degree(np.divide, temp, (J*J)), axes=(0, 1))[0, 0]
S = self.calcuteS(rlmatrix)
return numerator / S # 10. LRLGLE
def getLongRunLow(rlmatrix):
I, J = self.calcuteIJ(rlmatrix)
temp = self.apply_over_degree(np.multiply, rlmatrix, (J*J), axes=(0, 1))
numerator = np.apply_over_axes(np.sum, self.apply_over_degree(np.divide, temp, (J*J)), axes=(0, 1))[0, 0]
S = self.calcuteS(rlmatrix)
return numerator / S # 11. LRHGLE
def getLongRunHighGrayLevelEmphais(rlmatrix):
I, J = self.calcuteIJ(rlmatrix)
numerator = np.apply_over_axes(np.sum, self.apply_over_degree(np.multiply, rlmatrix, (I*I*J*J)), axes=(0, 1))[0, 0]
S = self.calcuteS(rlmatrix)
return numerator / S如果有什么不对之处,希望大家指正,谢谢!
作者:Manfestain
链接:https://www.jianshu.com/p/155e9ac7ab6f
来源:简书著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。

 少有人走的路
少有人走的路