少有人走的路由正切一定义，得tanθ=y/x，令x=1，则tangθ=y，所以tanθ的值就是纵坐标y。
下面来看看正切函数的图象。
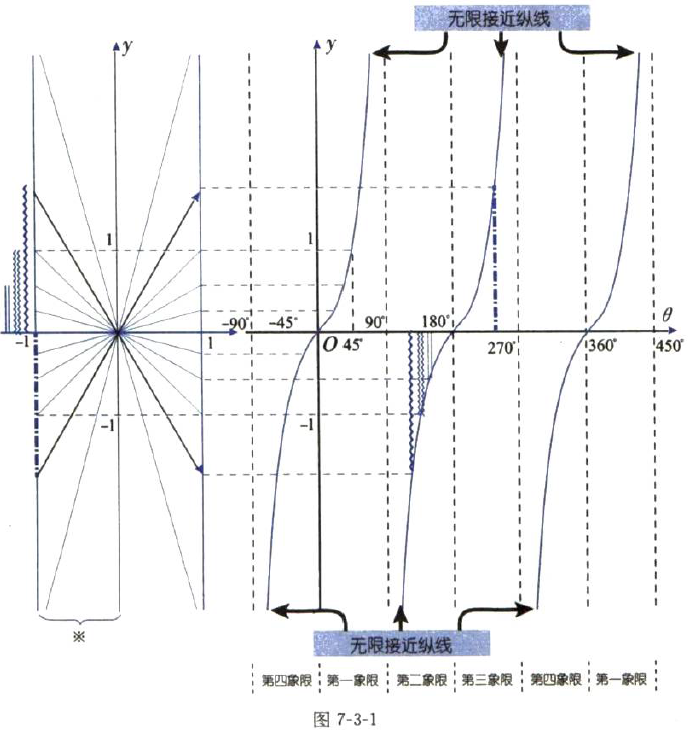
-90°到90°的区间内，直接把左图的y值平移到右图，图象呈光滑曲线。
tanθ的图象的一个非常显著特点是：不连续性。
当θ=±90°，±270°，±450°...时，图象是一段一段断开的，终边都落在y轴上。
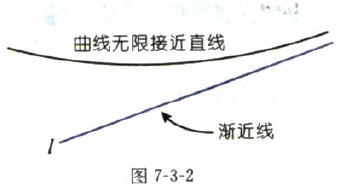
整条曲线处于无限接近某条纵线的状态，但永远不会和那条纵线相交。
通常，一条曲线无限接近某条直线L时，我们把那条直线L称为曲线的渐近线。
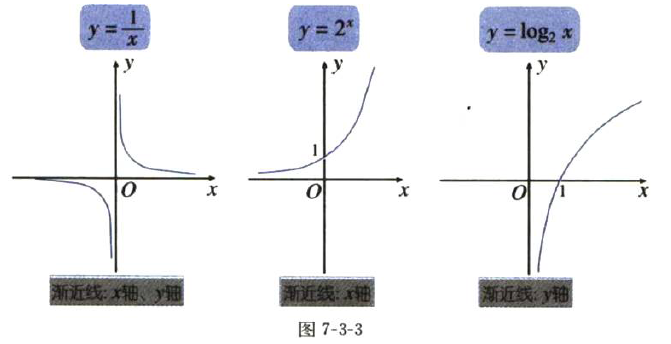
反比例函数的图象就是渐近线，y=1/x
指数函数和对数函数的图象也有渐近线。
tanθ也是一个周期函数，不是360°，而是180°，
它的图象是无限向上、下延伸，还是关于原点对称的图象。
所以
tanθ的周期为180° tanθ是奇函数
勇哥用Matlab绘制tan函数图像如下：
clc
%ezplot也可以绘制你指定的函数图像，简单好用
%ezplot('tan(x)',[-2*pi,2*pi])
x=-1.56:0.01:1.56;
y1=tan(x);
y2=2*tan(x);
plot(x,y1,x,y2)
title('正切函数图像')
xlabel('x')
ylabel('y')
grid on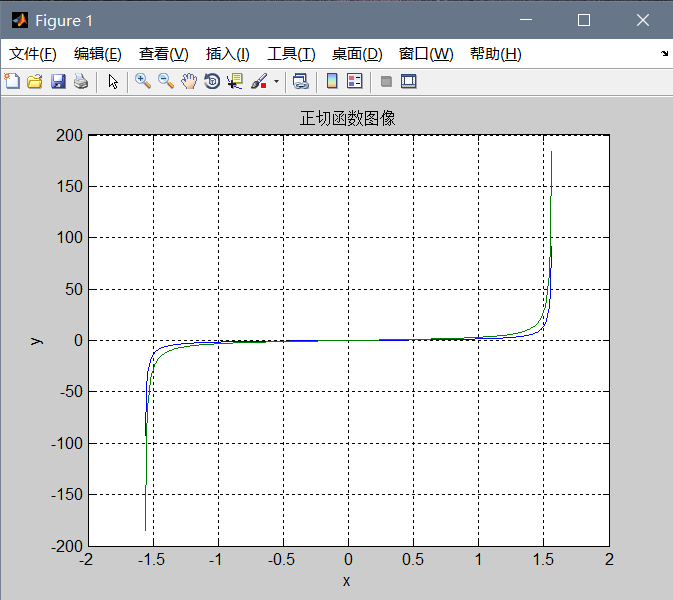
最后，我们把sin, cos, tan, ctang的四个图象放在一起：
x=0:pi/10:2*pi;
x2=[0+0.0001:pi/1000:2*pi]
y1=sin(x);
y2=cos(x);
y3=tan(x2);
y4=cot(x2);
subplot(2,2,1)
plot(x,y1);
title('sin')
grid on
axis([0,2*pi,-1.5,1.5])
subplot(2,2,2)
plot(x,y2);
title('cos')
grid on
axis([0,2*pi,-1.5,1.5])
subplot(2,2,3)
plot(x2,y3);
title('tan')
grid on
axis([0,2*pi,-50,50])
subplot(2,2,4)
plot(x2,y4);
title('ctan')
axis([0,2*pi,-50,50])
grid on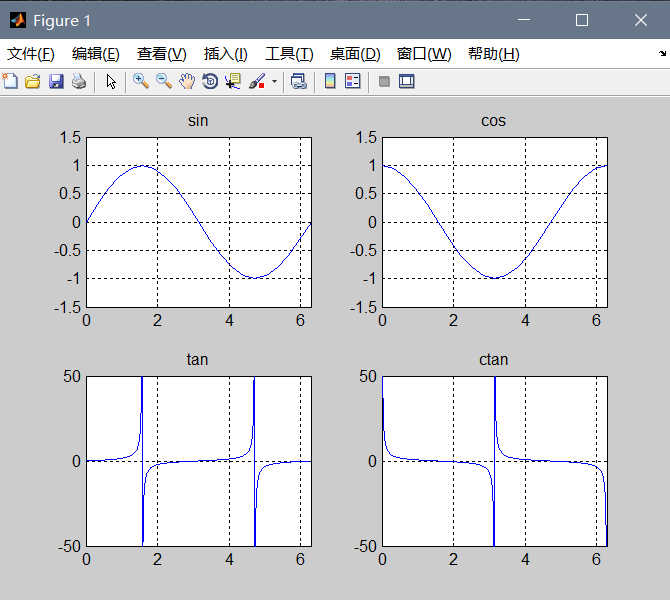
---------------------
作者：hackpig
来源：www.skcircle.com
版权声明：本文为博主原创文章，转载请附上博文链接！
本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：
