摘要
本文分析了人手臂关节的运动特点,据此确定了仿臂机器人自由度的分配。在分析和总结前人关于机器人运动学分析的基础上,详细地阐述了机器人建模、欧拉角选择以及运动学正反解的各种方法及其进展情况。比较了现有的计算方法的优缺点,并从中选出了一种适合本题目的一种运动学分析方法,为接下来的机器人分析计算打下基础。
关键词:四自由度 仿臂机器人 欧拉角 运动学正反解
目 录
摘要 III
目 录 IV
第1章 绪论 5
1.1 本课题现状 5
1.1.1 综述国内外研究现状 5
1.2 研究的主要成果 5
1.2.1 机器人运动学的正解算法 6
1.2.2 机器人运动学的逆解算法 9
1.3发展趋势 12
第2章 四自由度仿手臂机器人的建模 13
2.1机器人三维建模 13
2.2机器人模型参数确定 14
第3章 机械臂欧拉角选择 15
3.1求变换矩阵 15
3.2 欧拉角介绍 16
3.3欧拉角选择 17
3.3欧拉角计算 18
第4章 机器人位置正反解 20
4.1机械臂的正解与工作空间的求解 20
4.2机械臂的反解 21
参考文献 24
第1章 绪论
1.1 本课题现状
1.1.1 综述国内外研究现状
随着机器人技术的飞速发展,以及人们对机器人控制本质认识的加深,现在发展了越来越多具有感知、决策、交互行为的机器人,康复机器人、微操作机器人、军用机器人、水下机器人、娱乐机器人等等,这些机器人应用于不同任务和特殊环境下,在很多方面扩展了人类的工作能力,劳动条件也得到改善[2]。仿臂机器人也因此产生。人的手臂可以分成肩关节、腕关节和肘关节[1],其中肩关节可看作一个球副,有三个自由度,腕关节由桡腕关节和腕骨关节组成,能够实现屈、伸、展、收四个运动,因此具有四个自由度,肘关节可以实现小臂的俯仰和绕肘关节垂直轴的旋转。因此具有两个自由度。参考现有仿臂机器人的构型并结合人手臂的运动特点,确定本文的研究对象为四自由度的仿臂机器人,并且四个运动副均设计为转动。
对机器人的构型设计,运动学正反解是机器人设计需要讨论的关键问题之一,国内外的许多科学家也对此提出了许多解决办法。所谓机器人位置正解是指根据给定的关节变量求解机器人末端执行器的位置姿态的方法,相反,运动学反解是根据给定的机器人末端执行器的位置和姿态求解机器人各个关节变量的方法。1955年Denavit和Hartenberg提出的D-H法,采用四个独立变量(一个确定的关节对应有一个关节变量)来表示两个杆件之间相对位置,然后利用旋转矩阵的连乘积求得机器人的末端位姿[3];国内黄真提出利用螺旋系建立机器人的Plücker坐标来求解机器人的螺旋运动方程正解[4]。对于机器人的设计,其运动学反解更具有实际意义,但是其计算也比正解更复杂。国内荆学东[5]等人将基于运动螺旋的机器人运动学正解映射应用在搬运机器人的逆运动学问题中,廖启征[6]等人提出将四元素的复数形式应用于机器人运动学反解,文献[8]中提出满足piper条件的机器人可以将机器人的位置问题和姿态问题分别考虑,熊有伦分析了对于少自由度的机器人,用代数解和几何解的方法求解机器人的关节角[7]。
1.2 研究的主要成果
到目前为止,机器人运动学正解常用的方法有旋转矩阵法和螺旋理论,运动学逆解方法可分为两类:封闭解法和数值解法。在进行反解时,总是力求得到封闭解,因为封闭解法计算速度快,效率高,便于实时控制。封闭解法常用的方法有代数法、几何法、螺旋代数法、四元素代数法等,而数值解法不具有封闭解法的优点,但是如果机器人自由度较多时,为简化计算,有时也用数值解法进行计算。常用的有迭代法、Monte Carlo法等。下面本文就针对上面提到的解法一一解读。
1.2.1 机器人运动学的正解算法
1. 旋转矩阵法
基本思想:根据D-H法,在机器人各连杆上固接一个坐标系,然后利用一个4×4的齐次变换矩阵描述相邻两连杆的空间关系,从而推导出“手爪坐标系”相对于“参考系”的等价齐次变换矩阵,建立机器人的运动方程。下面以四自由度机器人为例,介绍这种方法法的应用。
根据连杆坐标系的建立原则:
1)坐标系{i-1}的z轴zi-1与关节轴i-1共线,指向任意;
2) 坐标系{i-1}的x轴xi-1与连杆i-1的公垂线重合,指向由关i-1到关节i,当ai-1=0时,取xi-1=±zi-1×xi-1 ;
3)坐标系{i-1}的y轴yi-1按右手法则规定,即yi-1=zi-1×xi-1。
建立各连杆的坐标系如下图:
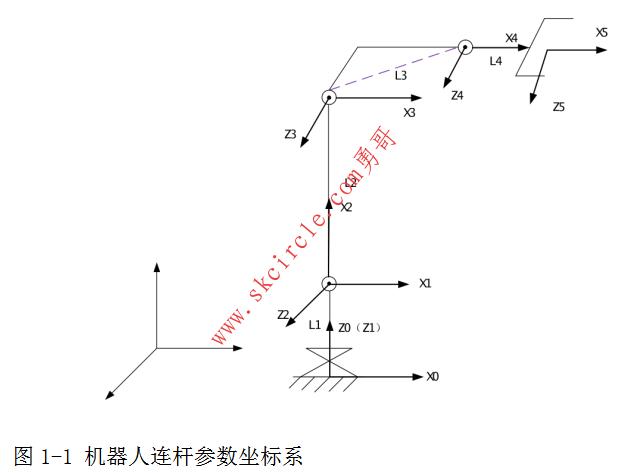
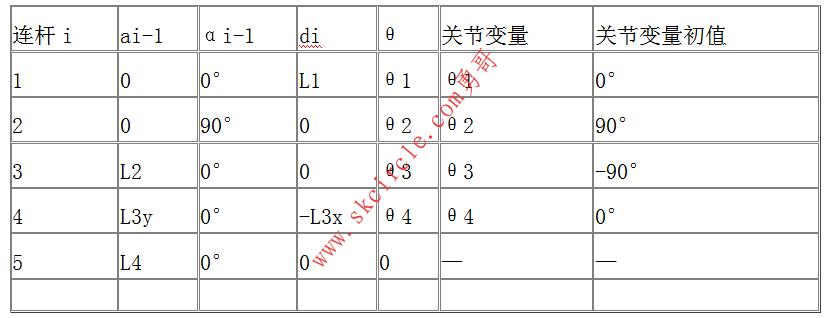
机器人的连杆参数表如下:
表1-1 机器人连杆参数表
根据连杆变换通式:



2. 螺旋理论
基本思想:适合线性组合规则的诸螺旋构成一个螺旋系。对于一个开链机器人,当所有运动副都表示为螺旋时,末端件的运动就是诸螺旋的线性组合,构成一个典型的螺旋系,机器人末端的位置就可以用从基系的原点到末端指定点的矢量来表示。
同样以四自由度为例,采用D-H 标记法,用两杆件轴线的公法线a12,a23 ,a34表示连杆的长度,其单位矢量为a12,a23, a34 ,a45相邻两杆间的偏距量用S1,S2,S3,S4,它取决于在同一个转动轴线上的两个公法线垂足之间的距离,铰链轴线分别用单位矢量S1,S2,S3,S4依次表示,相邻两转动轴的轴线之间的扭角为a12,a23,a34 ,相邻两杆之间的运动副相对转角以θi 表示。从机架开始,这些转角分别表示为φ1,θ2,θ3,θ4 。串联机器人的开链结构如下图所示:
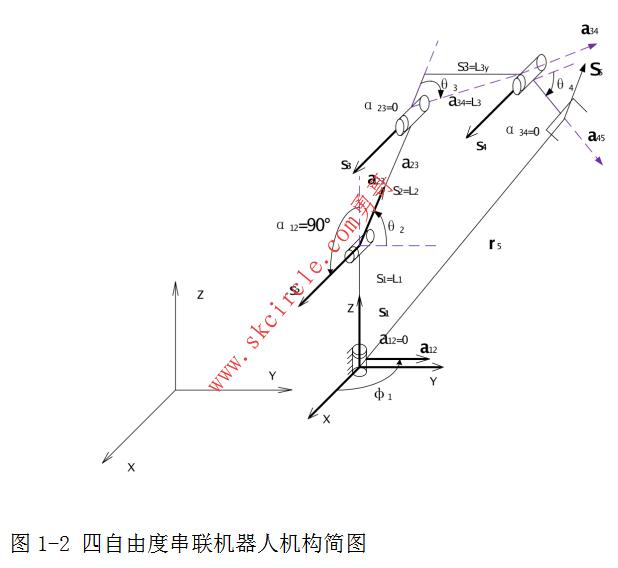
机器人手部的位置用手臂末端杆a34上的某指定点H的坐标来表示,其位置矢量r5可以表示为下面的矢量和:
r5=S1S1+a12a12+S2S2+a23a23+ S3S3+a34a34 +S3S3+a45a45 (3)
其中单位矢量S1,S2,S3,S4和a12,a23, a34 ,a45可以如下以坐标变换矩阵推得:
S1=(0 0 1)T
a12=[ZRφ1](0 0 1)T
这相当于将a12随坐标系O1X1Y1Z1绕Z轴转一个φ1角就得到a12相对固定坐标系的方向余弦,其中
[ZRφ1]=

类似的有
S2=[ZRφ1] [XRα12](0 0 1)T
a23=[ZRφ1] [XRα12][ZRθ2](1 0 0)T
S3=[ZRφ1] [XRα12] [XRα23](0 0 1)T
a34=[ZRφ1] [XRα12][ XRα23] [ZRθ3](1 0 0)T
S4=[ZRφ1] [XRα12] [XRα23] [XRα34](0 0 1)T
a45=[ZRφ1] [XRα12][ XRα23] [ XRα34] [ZRθ4](1 0 0)T
r5的三个坐标分量即为末端指定点H在基系中的位置投影。
1.2.2 机器人运动学的逆解算法
1. 封闭解法
1)代数法
代数法也称反变换法。求解运动学反解时,一般机器人的末端连杆位姿给定,这时用未知的连杆逆变换左乘,把关节变量分离出来,从而求解。具体计算过程如下(仍以四自由度机器人为例):




运用代数法求解机器人位置反解时,推导过程明确,易于理解,但计算量较大,是目前求解机器人位置反解的一种常用方法。
2. 几何法
当机器人自由度较少时,利用平面几何关系可以求出它的运动学反解。下面以平面3R机械臂为例进行分析。
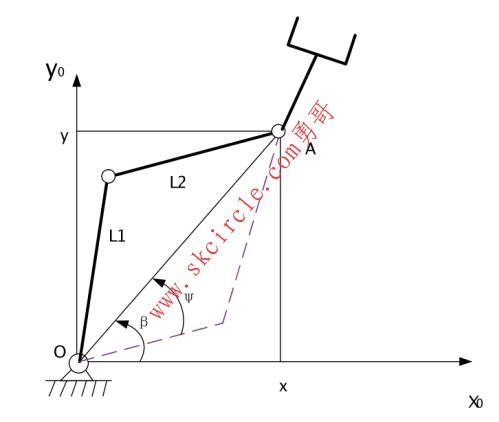
图1-3 3R机械臂机构简图
在L1、L2和OA组成的三角形内,应用余弦定理
x2+y2=L12+L22-2L1L2cos(180°+θ2) (8)
由此得
cosθ2= (x2+y2-L12-L22)/(2L1L2)
另外,目标点(x,y)需满足
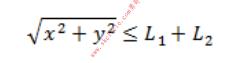
在满足解的存在性的前提下,可能有两个解(其中一个用虚线表示),
θ2=-θ2(-180°≤θ2≤0°)
β=Atan2(y,x)
cosψ=
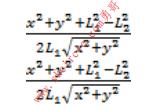
(0°≤θ2≤180°)
由此得出
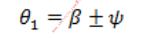
其中,当θ2<0°时,取“+”号,当θ2>0°时,取“-”号。
末端手爪的方位角Φ有三个关节角度之和确定,即
Φ=θ1+θ2+θ3
由此求出关节角θ3。
当自由度较多时,可采用旋量理论来进行求解。机器人的每一个轴线都可以看做是空间的一条线矢量,记为[L,M,N;P,Q,R],对于单位线矢量,有以下约束关系:
L2+M2+N2=1 (9)
LP+MQ+NR=0 (10)
于是,一个单位线矢量可以由四个独立变量来表示。应用直线平行、垂直的坐标计算式可以大大简化机器人运动学反问题的计算过程。
几何法的一个好处就是直观,各个连杆间的位置关系能够较容易表示出来,但是需要一定的空间想象力,而且当机器人各个关节轴线呈空间分布时,用几何法就不好求解了。
3. 四元素代数法
四元数是最简单的超复数,它由实数加上三个元素 i、j、k 组成,一般可表示为a + bi + cj + dk 。它们有如下的运算关系:
i2 = j2 = k2 = -1 ,
ij=k,jk=i,ki=j;
ji=-k,kj=-i,ik=-j。
每个四元数都是 1、i、j 和 k 的线性组合。
四元数的旋转矩阵具体形式如下:

其中,
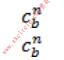
中的各个元素是关于末端执行器姿态α、β、γ的表达式,令上述矩阵的对应元素相等,可以得出当前姿态的四元素,从而能够将当前机器人的姿态表达出来。
4. 数值解法
(1)迭代法
迭代法依赖于初始点,可收敛于单一解,但收敛速度受限制,无法用于实时控制。王其军,杜建军提出了一种新的推导MO-TOMAN机器人逆运动学的方法,在解的推导过程中,采用双变量正切函数避免了解被丢失的可能性,回避了大量的逆矩阵相乘,简化了求解过程,大大减少了计算量。针对有多组逆解的情况,采用“最短行程”准则,选取一组最接近于当前操作臂的解[12]。董明晓等分析了PUMA机器人位置结构和姿态结构的特点,根据末端执行器位置矢量和姿态转换矩阵,在考虑臂形标志的基础上建立了逆运动学算法[13]。程永伦等基于变换矩阵中旋转子矩阵正交的特性,提出一种6R机器人运动学逆解算法。通过矢量运算,得到含有4个未知变量的4个常系数非线性方程,辅以其它方程,最终得到8组封闭解[14]。
(2)Monte Carlo法
Monte Carlo 法是用来解决数学和物理问题的非确定性的(概率统计的或随机的)数值方法,它是用一系列随机数来近似解决问题的一种方法,是通过寻找一个概率统计的相似体并用实验取样过程来获得该相似体的近似解的处理数学问题的一种手段。当所求问题的解是某个事件的概率,或者是某个随机变量的数学期望,或者是与概率、数学期望有关的量时,通过某种试验的方法,得出该事件发生的频率,或者该随机变量若干个具体观察值的算术平均值,通过它得到问题的解。这就是蒙特卡罗方法的基本思想。
在求解机器人运动学反解时,根据给定的末端执行器的工作空间确定各个关节角的大致范围,然后在范围内对各个关节的关节变量随机取数,利用MATLAB将机器人末端姿态的计算出来,验证末端位置是否能达到要求的位置,如不满足要求,需舍去,再重复循环,直到将所有的可能解取出,然后根据“多移动小关节,少移动大关节”、“最短路径”、受力最好、功率最省、回避障碍等原则选出一组最优解。
当由机器人的齐次变换矩阵得到的关于关节变量的方程是非线性方程时,可以采用这种方法,但是其计算量太大,必须借助计算机来进行计算。
1.3发展趋势
一个好的算法必须是易于操作,过程简便,现在常用的串联机器人位置正解方法是齐次变换矩阵,反解方法一般因机器人关节分布的不同而多种多样,没有统一的解法。在未来的机器人位置反解算法的发展中,由于有了计算机这个强大的计算武器,所以我们可以根据实际机器人连杆结构模型去建立反解方程,求其封闭解,或者采用数值法,将更精确的算法应用到其中,求得近似解。
第2章 四自由度仿手臂机器人的建模
2.1机器人三维建模
本小组所承担的课程任务是设计一个四自由度的仿手臂机器人,其在工程实际应用中的实例如下图所示:
图2-1 四自由度仿手臂机器人实体图
结合工程实例与课程任务,我们设计了一种4R型机器人,该机器人由由4个回转关节组成,有4个自由度,可用于完成搬运、焊接、喷漆、检测、装配等工艺操作,是一种典型的操作机器人。利用Solidworks对机器人进行了三维建模,其三维模型图如下图所示:
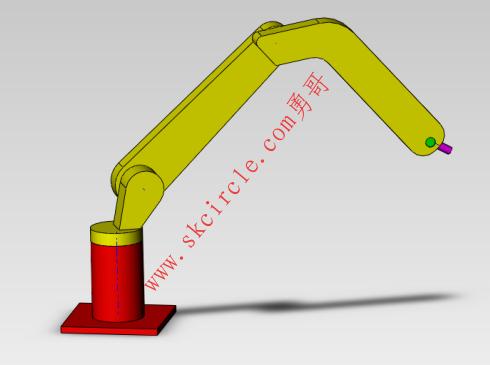
图2-2四自由度仿手臂机器人三维模型图
2.2机器人模型参数确定
假定机器人的总臂长L为2000mm,通过考虑机械臂的工作空间、灵活度以及比耗值等因素,我们确定了机械臂的杆长,其中L1=0.1L=200mm,L2=0.45L=900mm,L3=0.4L=800mm,L4=0.05L=100mm。其结构简图如下图所示:
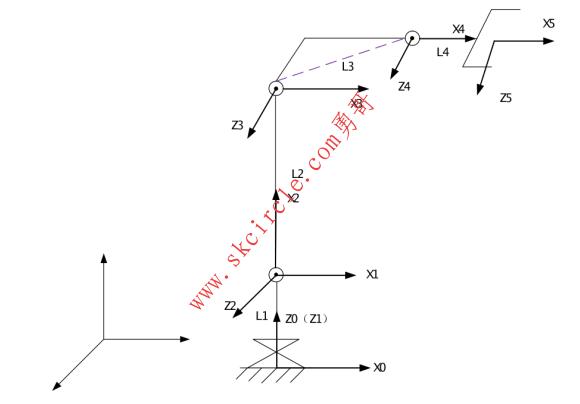
图2-3 机器人连杆参数坐标系
第3章 机械臂欧拉角选择
3.1求变换矩阵
该机器人为四自由度串联仿手臂机器人,由四个转动关节组成。关节1的轴线为铅直方向,关节2、3、4的轴线为水平方向,各连杆坐标系如图1所示,相应的连杆参数如表1所示。
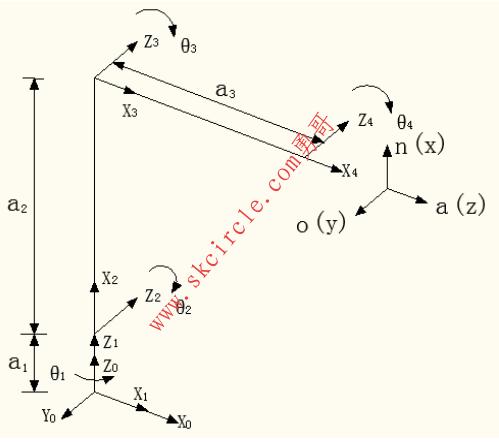
图3-1四自由度串联仿手臂机器人的各连杆坐标系
表3-1 四自由度串联仿手臂机器人的连杆参数
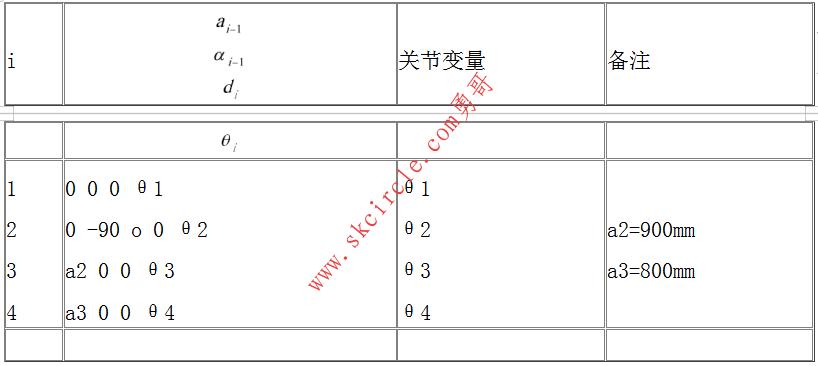
利用公式可以求出个连杆的变换矩阵:



3.2 欧拉角介绍
描述构件的空间方位最常用的是3×3的方向余弦矩阵R和4×4的位姿矩阵。方向余弦矩阵表示了以连于空间物体的动坐标系SD的方向余弦,
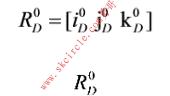
是正交矩阵,在他的9个元素中有6个约束条件,因而只有3个元素是独立的。
虽然特别适合做矩阵运算的方向余弦矩阵和位姿矩阵,作为坐标系之间的映射和作为点的运动算子都得到广泛的应用,但是方向余弦矩阵对于描述物体在空间的姿态不是很方便。一方面,要计算多达9个参数。另一方面,它很难直观的形成物体在空间的具体方位。
欧拉角表示是一种描述物体空间姿态的角度给定法,它是位姿坐标系绕动坐标系进行三次转动所得到的,因此只需求出三个角度即可。
欧拉角根据转动的排列顺序不同,共有以下12种不同的欧拉角组合。
表3-2 12种不同的欧拉角组合
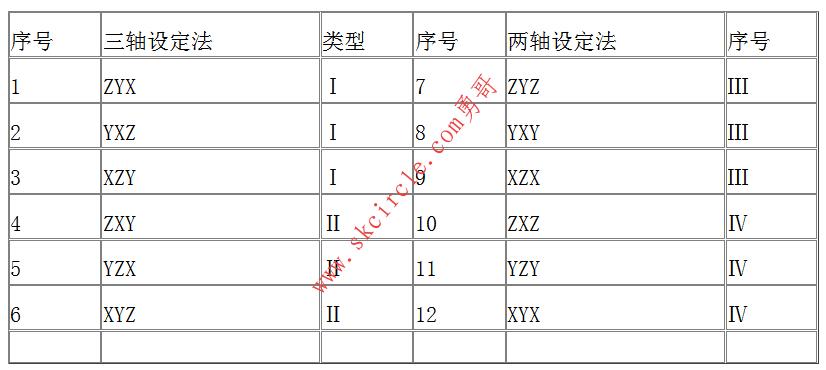
分析表中的12组欧拉角,可以发现这些欧拉角很多是相似的。如ZYX、YXZ、XZY三者是相似的,它们只是按照XYZ的反序排列,只是起始轴不同。而XYZ、YZX、ZXY三者是按照XYZ的正序排列,只是起始轴不同。因此在这12种不同的欧拉角中只有4种是真正的不同,它们是,ZYX、ZXY、ZYZ、ZXZ。
3.3欧拉角选择
如上文所示,欧拉角从Ⅰ、Ⅱ、Ⅲ、Ⅳ四种类型轴旋转中选择,而从串联机器人所建立的坐标系(如图1)所示,该机器人没有绕X轴旋转的运动,因此排除含有绕X轴旋转的欧拉角组合,最终欧拉角从ZYZ型和YZY型中选择。
在使用欧拉角对于物体的姿态进行描述的过程中,为了突出的表示运动物体的方向和姿态,称xy平面为动平面,XY为固定平面。运动和静止两个平面的交线定义为“脊线”,脊线能突出的反映了动平面的方位,是我们分析运动平面方位或姿态的重要依据。
用O-XYZ表示固定坐标系,o-xyz表示动坐标系,对应轴也相互重合。下面对于YZY型和ZYZ型进行比较。
(1)YZY型欧拉角
坐标轴转动(0 0 0),物体的运动平面xy与XY平面平行。
坐标轴转动(α 0 0),脊线是y轴,且它与Y轴重合,经过一次转动到达此状态。
坐标轴转动(α β 0),脊线即不与x轴重合也不与y轴重合,但可以通过y轴反转β角来找到脊线的位置。
坐标轴转动(α β γ),脊线即不与x轴重合也不与y轴重合,也无法通过坐标轴反转已知角度来找到脊线的位置。
因此,这种方式下直接给出三个欧拉角(α β γ)很难直接依赖三个角度来直接判断脊线,以确定姿态。
(2)ZYZ型欧拉角
坐标轴转动(0 0 0),物体的运动平面xy与XY平面平行。
坐标轴转动(α 0 0),物体绕Z轴转动α角,运动平面xy与XY平面相对位置不变。
坐标轴转动(α β 0),脊线与y轴重合,经过两次转动到达此状态。
坐标轴转动(α β γ),脊线即不与x轴重合也不与y轴重合,但可以通过坐标轴y反转γ角来找到脊线的位置。
因此,这种方式下直接给出三个欧拉角(α β γ)可以直接依赖三个角度来直接判断脊线,以确定姿态。
所以,最终选择ZYZ型欧拉角作为末端姿态的描述。
3.3欧拉角计算
ZYZ型欧拉角的描述,为先绕动坐标系的Z轴转动α角,再绕Y转动β角,最后绕Z转动γ角。
根据从左到右的原则,可以求得旋转矩阵:




第4章 机器人位置正反解
4.1机械臂的正解与工作空间的求解
我们的串联机器人是四自由度的机械手臂。其机构简图1如下:
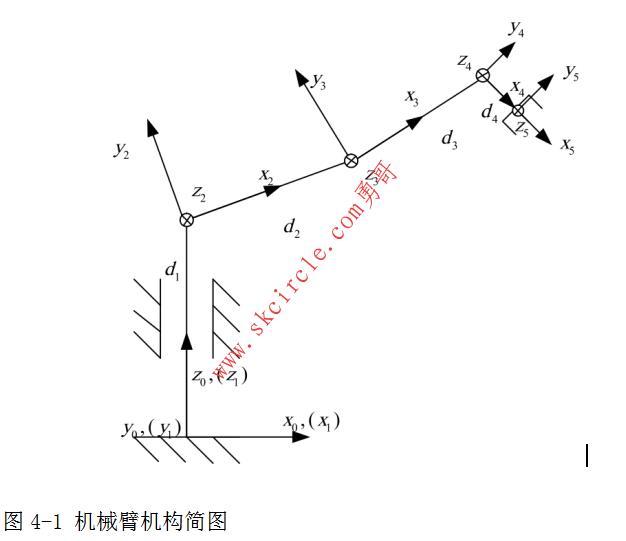


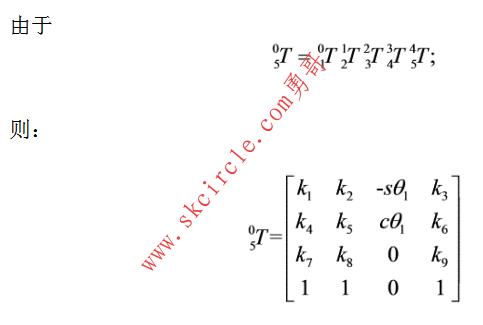
其中:


4.2机械臂的反解
运动学反解的方法有很多,这里我们选用向量法和反变换法。具体如下:
1、向量法
由于除了第一根杆件之外,其他的杆件位于一个平面内,可以看成是平面四杆机构来处理,这样问题便得以简化。
设末端执行机构的位置为

有两组确定的解。其反解精度可以控制在%5范围内。
2、反变换法
机构的运动方程可以写成:




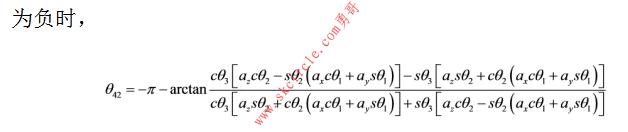
参考文献
[1] 杜金霞.仿人臂通用机器人的研究[D].兰州理工大学.2008.5
[2]李晓君.工业机器人:“英雄”有用武之地[J].中国石化报.2012.5.17
[3]熊有伦.机器人技术基础[M].华中科技大学出版社1996.8
[4].黄真等,高等空间机构学[M].高等教育出版社。2006.6
[5]荆学东等,应用基于运动螺旋的机器人正解映射求解搬运机器人的逆运动学问题[J].陕西科技大学学报,2008.12
[6]廖启征等,四元数的复数形式及其在6R机器人反解中的应用[J].系统科学与数学.2009.9
[7]熊有伦,机器人学[M],华中科技大学出版社,
[8]Robot manipulators and control systems,2007
[9]戴巍,六自由度并联机器人运动学分析[J],东华大学,2006
[10] Frank L.Lewis , Robot manipulators control theory and practice[M],University of Manchester Institute of Science and Technology,2004
[11] 陈伍林,基于四元素法的捷联惯导姿态更新算法[J],北京安达维尔公司内刊,2012
[12] 王其军,杜建军. MOTOMAN机器人逆运动学新分析[J]. 哈尔滨工业大学学报. 2010, 42(3): 451-454
[13] 董明晓,陈美华. PUMA机器人逆运动学分析[J]. 山东建筑工程学院学报. 2000, 15(4): 63-66
[14] 程永伦,朱世强等. 基于旋转子矩阵正交的6R机器人运动学逆解研究[J]. 机器人. 2008, 30(2): 160-164
[15] Miros law Galicki , Generalized Kinematic Control of Redundant Manipulators[J], Friedrich Schiller University Jena,2007

 少有人走的路
少有人走的路