紧接上一篇:三角函数:图像和性质关系
这一篇我们来推导一些常用的三角函数公式,主要方便以后图形程序中的计算。
1.余弦定理公式
余弦定义主要作用是依靠已知三角形的两条边及其夹角,求第三边的情况,如下图:
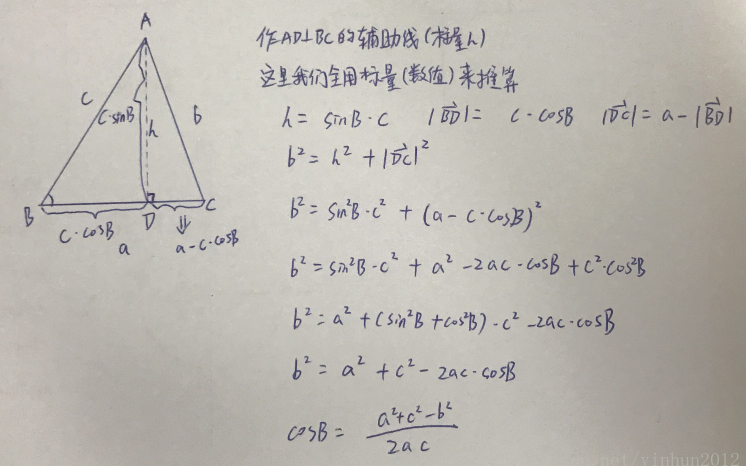
这里我们不处理向量(矢量)运算,单纯的从标量数值长度的推算入手,建立垂线后,得到的直角三角形ADC,可以通过勾股定理(前面推过)和sin²α+cos²α=1得到上面两个公式,后面的公式对我们求角度有很大帮助,而且这两个公式对后面图形方面计算会起到很大的帮助。
1.正弦定理的推导,前面有余弦定理,那么肯定就有一个对应的正弦定理了。
ps:这里要了解一个外接圆的概念,就是三角形△ABC的三个顶点都在一个圆上,那么这个圆就是△ABC的外接圆,其实这个也好反向理解,比如我们先画一个圆,然后任意在圆上取三点,连接三点就是一个三角形,但是假如我们不知道三角形的外接圆,要怎么去绘画和证明呢,如下图:
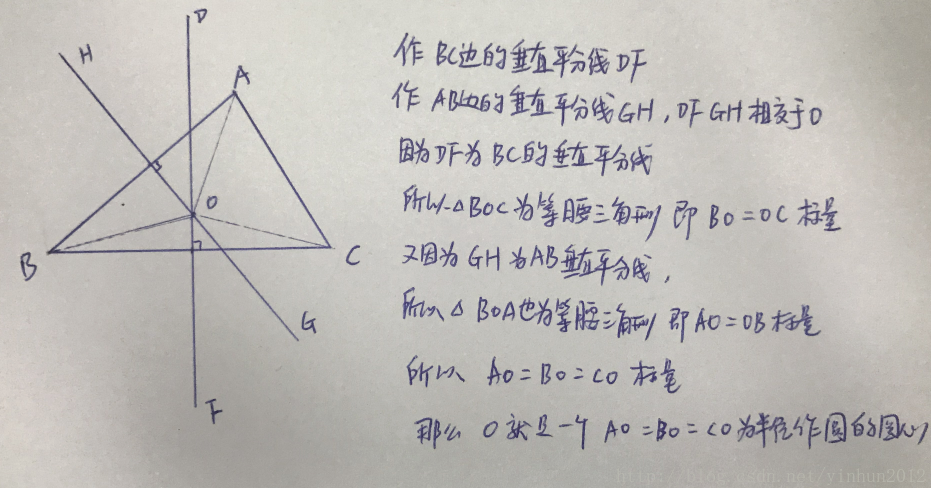
上面我们通过两条垂直平分线,就能得到△AOB和△BOC,且两三角形为等腰三角形(这个很好看出来,△AOB被平分成共边的两个一样的直角三角形),那么OA = OB = OC,所以O为圆心做半径OA的圆就是外接圆了。
接下来继续推导正弦公式,如下图:
上面我们推导了外接圆,那么接下来我们只需要建立等腰三角形△AoB △AoC △ BoC,将∠A转化成∠θ,就能得到上面的正弦定理了。
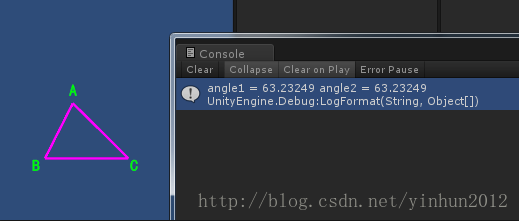
接下来到实际程序应用环节了,其实在实际项目开发中,余弦定理我用的还是挺多的,比如:
using System.Collections;
using System.Collections.Generic;
using UnityEngine;
public class AngleFunc : MonoBehaviour {
public GameObject PointA;
public GameObject PointB;
public GameObject PointC;
void Start()
{
{ //构建一个三角形
GameObject[] gos = new GameObject[3];
gos[0] = PointA;
gos[1] = PointB;
gos[2] = PointC;
for (int i = 0; i < gos.Length; i++)
{
LineRenderer line = gos[i].AddComponent<LineRenderer>();
line.positionCount = 2;
line.startWidth = 0.1f;
line.endWidth = 0.1f;
int index = i + 1;
if (index >= gos.Length)
index = 0;
line.SetPosition(0, gos[i].transform.position);
line.SetPosition(1, gos[index].transform.position);
}
}
//用余弦定理计算角度
Vector3 AB = PointB.transform.position - PointA.transform.position;
Vector3 BC = PointC.transform.position - PointB.transform.position;
Vector3 AC = PointC.transform.position - PointA.transform.position;
//计算∠A的夹角
float angle1 = Mathf.Acos((getVectorLengthPow2(AB) + getVectorLengthPow2(AC) - getVectorLengthPow2(BC)) / (2 * Mathf.Sqrt(getVectorLengthPow2(AB) * getVectorLengthPow2(AC)))) * Mathf.Rad2Deg;
//用自带的api计算角度
float angle2 = Vector3.Angle(AB, AC);
#if UNITY_EDITOR
Debug.LogFormat("angle1 = {0} angle2 = {1}", angle1, angle2);
#endif
}
private float getVectorLengthPow2(Vector3 vec)
{
return Mathf.Pow(vec.x, 2) + Mathf.Pow(vec.y, 2) + Mathf.Pow(vec.z, 2);
}
}代码比较少,直接贴上来了,主要就是用三角函数计算夹角值,其实unity中有自带的api,但是我们要知道公式的推导来源
---------------------
作者:羊羊2035
来源:CSDN
原文:https://blog.csdn.net/yinhun2012/article/details/79391444
版权声明:本文为博主原创文章,转载请附上博文链接!

 少有人走的路
少有人走的路