下面文章引用自:
中国科学院自动化研究所
模式识别国家重点实验室
http://www.nlpr.ia.ac.cn/english/rv
包括如下的内容:
1、引言:什么是摄相机标定
2、摄相机标定方法的分类
3、传统摄相机标定方法(或利用景物信息的标定方法)
4、主动视觉摄相机标定方法
5、摄相机自标定方法
1、引言
视觉目的
三维重建是人类视觉的主要目的,也是计算机视觉的最主要的研究方向. (Marr 1982)
所谓三维重建就是指从图象出发恢复出空间点三维坐标的过程。
三维重建的三个关键步骤
• 图象对应点的确定
• 摄像机标定
• 二图象间摄像机运动参数的确定
坐标系
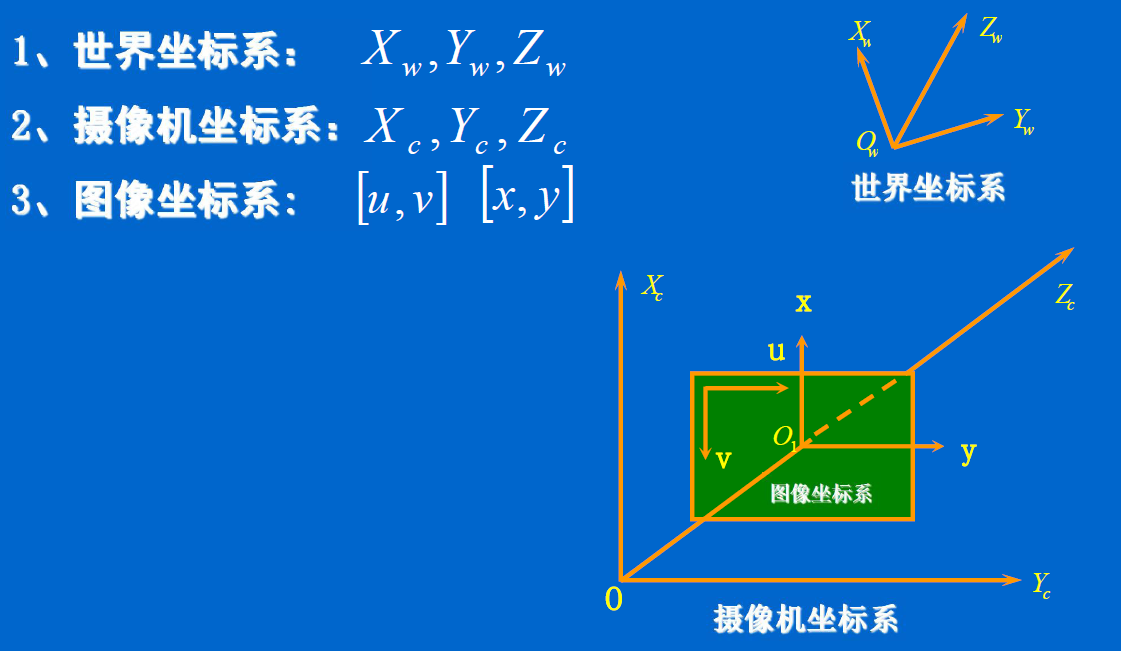
图像数字化
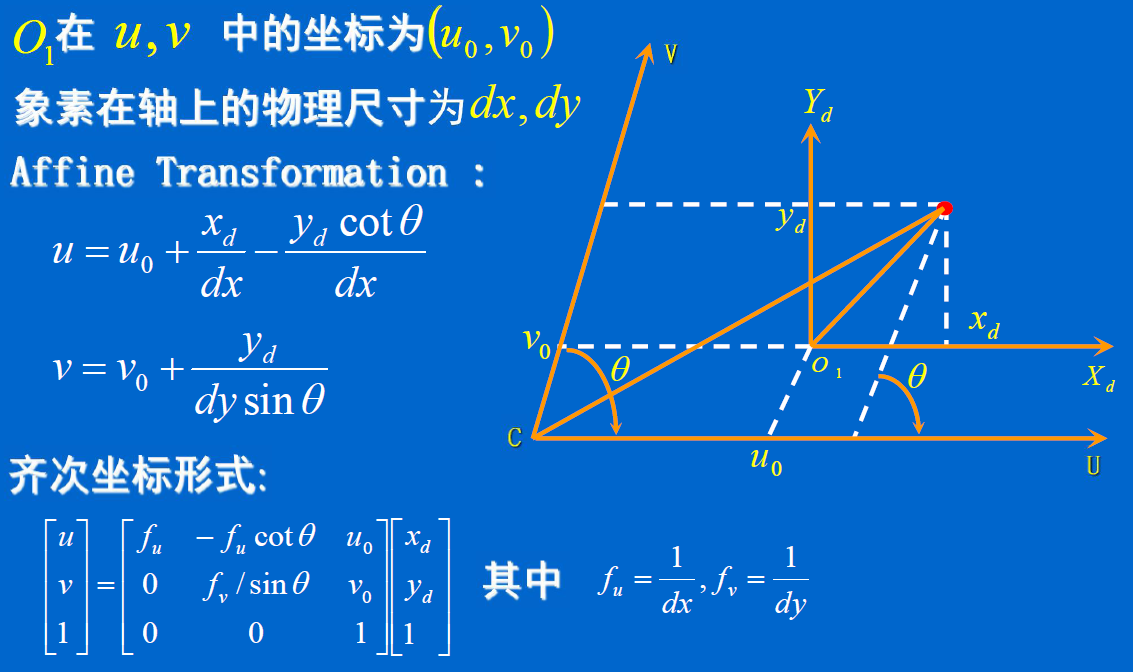
摄像机的内参数矩阵 K
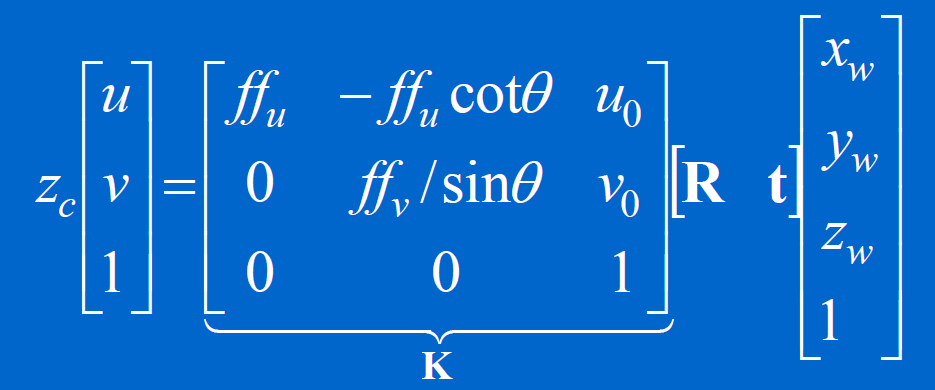
2、摄相机标定方法分类
分三类
• 传统摄像机标定方法
• 主动视觉摄像机标定方法
• 摄像机自标定方法
1. 传统的摄像机标定方法
特点
利用已知的景物结构信息。常用到标定块。

• 优点
可以使用于任意的摄像机模型,标定精度高
• 不足
标定过程复杂,需要高精度的已知结构信息。
在实际应用中很多情况下无法使用标定块。
2. 主动视觉摄像机标定方法
• 特点
已知摄像机的某些运动信息
• 优点
通常可以线性求解,鲁棒性比较高
• 不足
不能使用于摄像机运动未知和无法控制的场合
3. 摄像机自标定方法
• 特点
仅依靠多幅图像之间的对应关系进行标定
• 优点
仅需要建立图像之间的对应,灵活性强,潜在
应用范围广。
• 不足
非线性标定,鲁棒性不高
3、摄像机传统标定方法
3.1、DLT方法
3.2、RAC方法
3.3、张正友的平面标定方法(ICCV, 1999)
3.4、孟胡的平面圆标定方法(PR, 2003)
3.5、吴毅红等的平行圆标定方法(ECCV, 2004)
3.1、直接线性变换(DLT变换)
DLT变换
Abdal-Aziz和Karara于70年代初提出了直接线性变换像机定标的方法,他们从摄影测量学的角度深入的研究了像机图像和环境物体之间的关系,建立了像机成像几何的线性模
型,这种线性模型参数的估计完全可以由线性方程的求解来实现。
直接线性变换是将像点和物点的成像几何关系在齐次坐标下写成透视投影矩阵的形式:
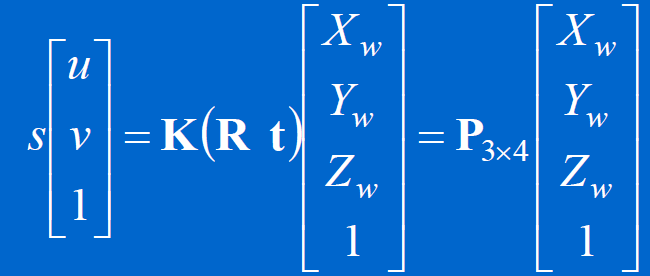
![]()


当已知 个空间点和对应的图像上的点时,可以得到一个含有2* N个方程的方程组:
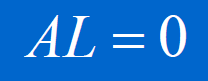




3.2、R. Tsai 的 RAC的定标算法
80年代中期Tsai提出的基于RAC的定标方法是计算机视觉像机定标方面的一项重要工作,该方法的核心是利用径向一致约束来求解除 (像机光轴方向的平移)外的其它像机外参数,然后再求解像机的其它参数。基于RAC方法的最大好处是它所使用的大部分方程是线性方程,从而降低了参数求解的复杂性,因此其定标过程快捷,准确。
•像机模型
•径向一致约束
•定标算法
像机模型


径向一致约束

定标算法
定标步骤:

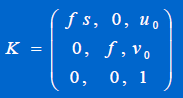
定标算法——步骤一
求解像机外参数旋转矩阵 R 和 x 、y 方向上的平移
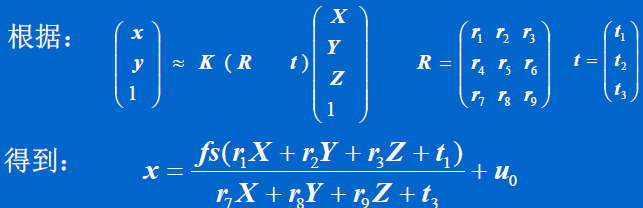
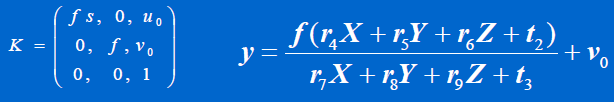




将 x, y 的表达式代入,并将上一步中求出的 R, t1, t2 的值代入,得:
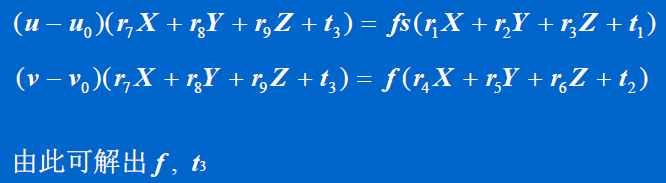

3.3、张正友的平面标定方法
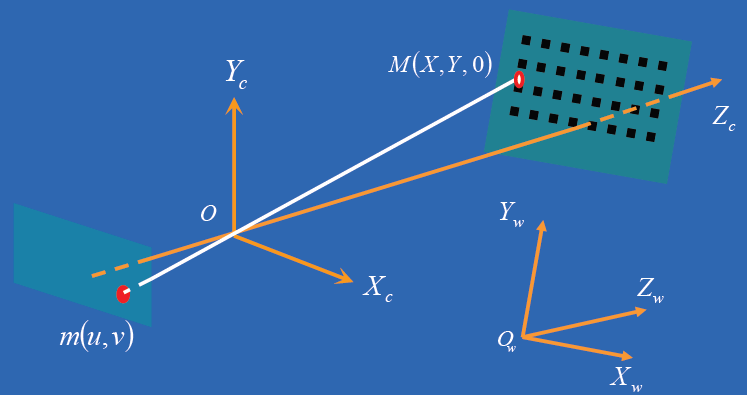



算法描述
张正友方法
1. 打印一张模板并贴在一个平面上
2. 从不同角度拍摄若干张模板图象
3. 检测出图象中的特征点
4. 求出摄像机的内参数和外参数
5. 求出畸变系数
6. 优化求精
张正友的平面标定方法是介于传统标定方法和自标定方法之间的一种方法。它既避免了传统方法设备要求高,操作繁琐等缺点,又较自标定方法精度高,符合办公、家庭使用的桌
面视觉系统(DVS)的标定要求。
张的方法是需要确定模板上点阵的物理坐标以及图像和模板之间的点的匹配,这给不熟悉计算机视觉的使用者带来了不便。
3.4、孟晓桥、胡占义的圆标定方法

从至少三个不同方位拍摄模板图象,根据射影不变性计算出每幅图象上的圆环点像的坐标,得到关于内参数矩阵的至少六个方程,
即可解出所有内参数。
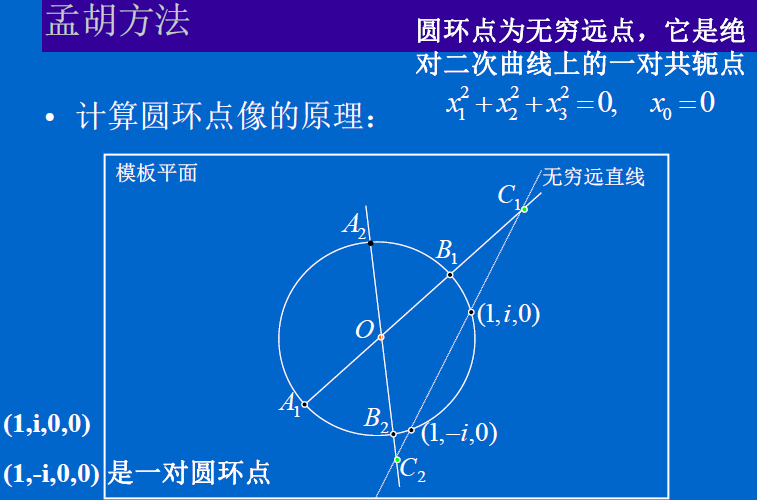

孟胡的方法与张的方法相比:
过程相似;
所用的模版不同,孟胡的方法基于曲线拟合(稳定),并且不需要任何匹配,而张的方法基于点,需要匹配模版的点和图像点。
3.5、吴等的平行圆标定方法

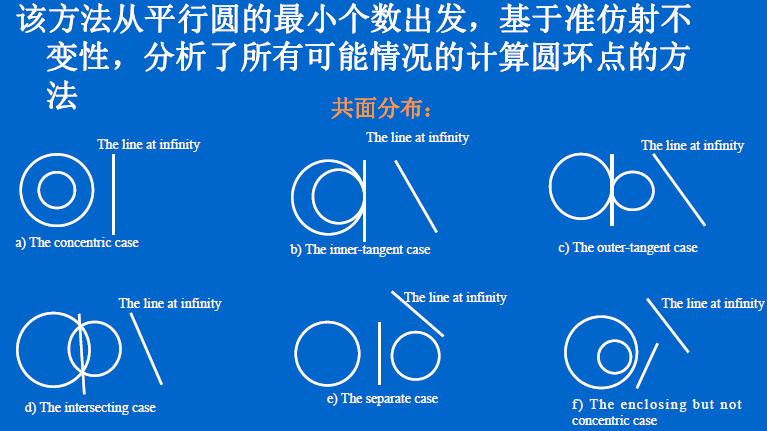


该方法和以往的基于圆的标定方法相比:
(1). 从最小个数出发;
(2). 计算圆环点图像简单;
(3).只需要从拟合的二次曲线出发, 不需要任何匹配, 不需要计算圆心;
(4). 应用场合广泛, 不仅仅限于平面的情形. 可应用基于转盘的重构。

4、主动视觉标定方法
胡占义等的主动视觉标定方法
• 基于平面单应矩阵的正交运动方法
• 基于外极点的正交运动方法


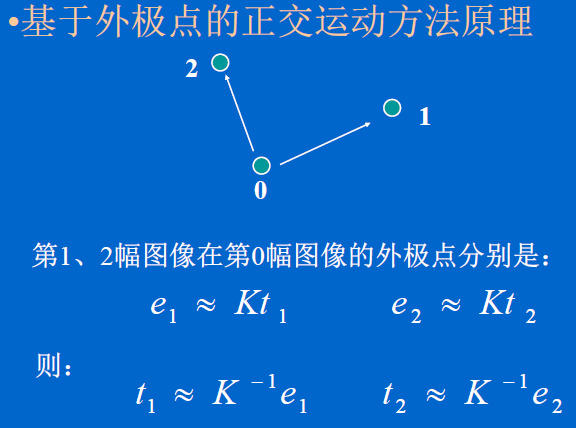

这两种主动视觉标定方法与最经典的主动视觉标定方法(马颂德的三正交运动法)相比,具有如下优点:
• 照相机的二正交运动比三正交运动更容易实现。
• 可以求解摄像机的所有5个内参数,马颂德的方法可以求解4个内参数。
5、摄像机自标定方法
5.1、预备知识:
什么是摄像机自标定 ?
为什么要对摄像机进行自标定 ?
对极几何……
5.2、基于Kruppa方程的自标定方法
5.3、基于绝对二次曲面、无穷远平面的自标定方法
5.4、几种自标定方程的关系
5.1、预备知识
什么是自标定?
为什么要进行自标定?
实际应用的需求,主要应用场所的转移
优缺点:
优点:灵活,方便
缺点:精度不太高,鲁棒性不足
自标定的基本假设及任务
1、假定图象点之间的对应关系已经确定。
2、一般来说,认为在拍摄不同图象时,摄像机的内参数没有发生变化
3、所谓的自标定,就是要标定摄像机的内参数矩阵K
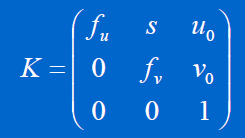




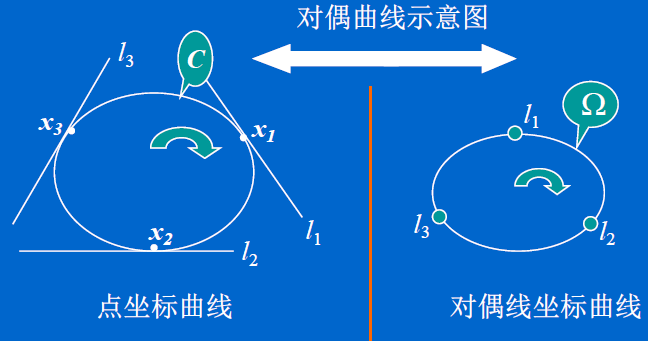
欧几理得空间下的投影矩阵
如果X 为空间某一点,两摄像机间的坐标变换为:

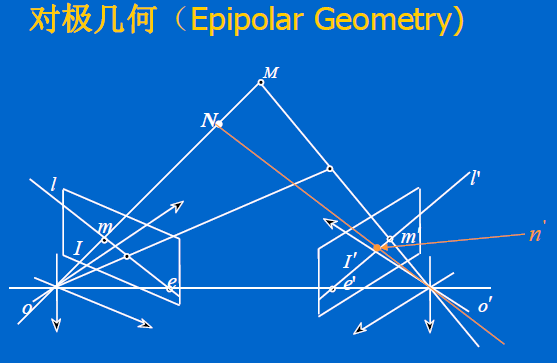


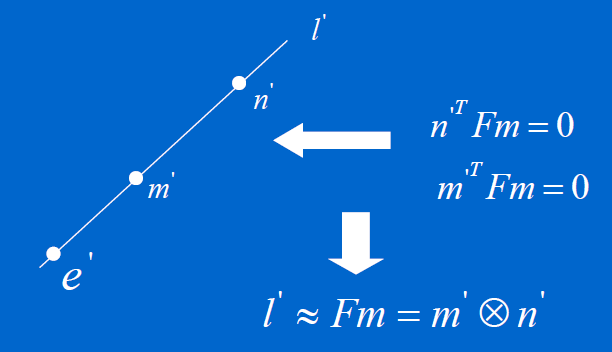
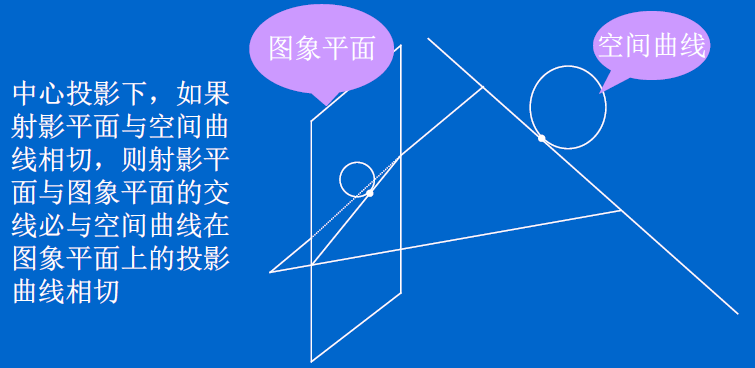


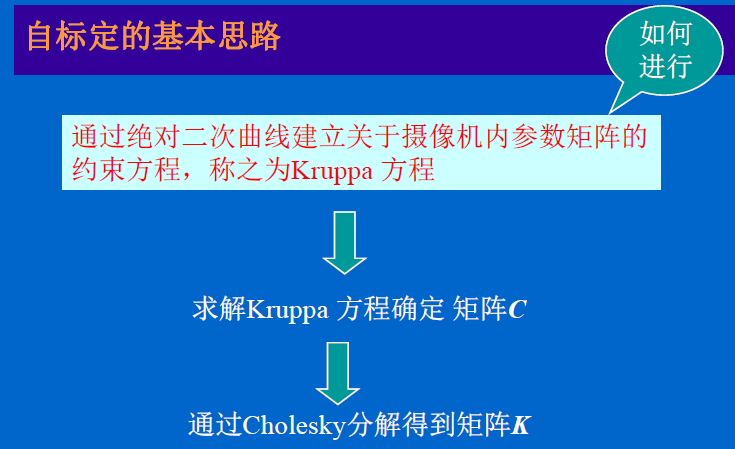
5.2、基于Kruppa方程的自标定方法
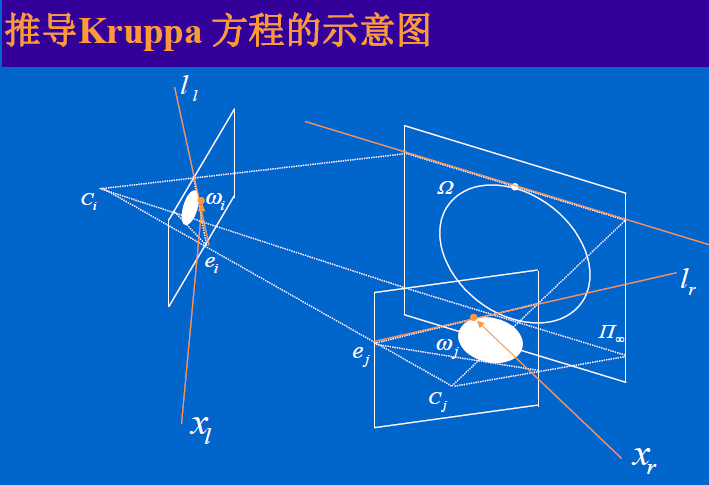



5.3、基于绝对二次曲面、无穷远平面的自标定方法




5.4、几种自标定方程的关系
关系
基于绝对二次曲面的标定方程与基于无穷远平面的标定方程完全等价。
由绝对二次曲面的标定方程或无穷远平面的标定方程可以推出 Kruppa 方程。反之,对Kruppa 方程添加一个方程后,可以推出绝对二次曲面的标定方程或无穷远
平面的标定方程。
标定板介绍
产品特性:
1. 确认光学系统的性能,复原相机模型的3D空间至2D空间的一一对应关系。

标定的作用其一就是为了求取畸变系数(因为经过镜头等成像后,或多或少都有畸变),其二是为了得到空间坐标系和图
像坐标系的对应关系。
2. 定位精度高达0.001mm;
3. 经典棋盘格标定板,实心圆阵列标定板,网格标定板可兼容于大多数图像处理算法的标定算法。

 少有人走的路
少有人走的路