命名空间:
netMarketing.graphics
netMarketing.MathAnalysis
功能: 数学矩阵类,已重载了主要的运算符
功能详细说明:
提供了两个矩阵类,一个是netMarketing.MathAnalysis.Matrix。
另一个是netMarketing.graphics.Matrix
功能是类似的。
这些数学矩阵类 都重载了 +- */ += == -= /= *= 运算符
注意:以下函数表以及示例都使用的是netMarketing.MathAnalysis.Matrix
常用函数列表:
public Matrix()
/// 指定行列构造函数
/// @param nRows - 指定的矩阵行数
/// @param nCols - 指定的矩阵列数
public Matrix(int nRows, int nCols)
/// 指定值构造函数
/// @param value - 二维数组,存储矩阵各元素的值
public Matrix(double[,] value)
/// 指定值构造函数
/// @param nRows - 指定的矩阵行数
///@param nCols - 指定的矩阵列数
///@param value - 一维数组,长度为nRows* nCols,存储矩阵各元素的值
public Matrix(int nRows, int nCols, double[] value)
///方阵构造函数
///@param nSize - 方阵行列数
public Matrix(int nSize)
/// 方阵构造函数
///@param nSize - 方阵行列数
///@param value - 一维数组,长度为nRows* nRows,存储方阵各元素的值
public Matrix(int nSize, double[] value)
/// 拷贝构造函数
/// @param other - 源矩阵
public Matrix(Matrix other)
属性: 矩阵行数
public int Rows { get; private set; }
索引器: 访问矩阵元素
public double this[int row, int col]
/// 属性: Eps
public double Eps { get; set; }
/// 初始化函数
public bool Init(int nRows, int nCols)
/// 设置矩阵运算的精度
public void SetEps(double newEps)
/// 取矩阵的精度值
public double GetEps()
/// 重载 + 运算符
public static Matrix operator +(Matrix m1, Matrix m2)
///重载 - 运算符
public static Matrix operator -(Matrix m1, Matrix m2)
///重载 * 运算符
public static Matrix operator *(Matrix m1, Matrix m2)
///重载 double[] 运算符
public static implicit operator double[](Matrix m)
///将方阵初始化为单位矩阵
public bool MakeUnitMatrix(int nSize)
///将矩阵各元素的值转化为字符串, 元素之间的分隔符为",", 行与行之间有回车换行符
public override string ToString()
///将矩阵指定行中各元素的值转化为字符串
public string ToStringRow(int nRow, string sDelim)
///将矩阵指定列中各元素的值转化为字符串
public string ToStringCol(int nCol, string sDelim /*= " "*/)
///设置矩阵各元素的值
public void SetData(double[] value)
///设置指定元素的值
public bool SetElement(int nRow, int nCol, double value)
///获取指定元素的值
public double GetElement(int nRow, int nCol)
///获取矩阵的列数
public int GetNumColumns()
///获取矩阵的行数
public int GetNumRows()
///获取矩阵的数据
public double[] GetData()
public double[,] GetArrayData()
///获取指定行的向量
public int GetRowVector(int nRow, double[] pVector)
///获取指定列的向量
public int GetColVector(int nCol, double[] pVector)
public Matrix GetSubMatrix(int subRow, int subCol)
public Matrix GetSubMatrix(int subRowCols)
///给矩阵赋值
public Matrix SetValue(Matrix other)
///判断矩阵否相等
public override bool Equals(object other)
///实现矩阵的加法
public Matrix Add(Matrix other)
///实现矩阵的减法
public Matrix Subtract(Matrix other)
///实现矩阵的数乘
public Matrix Multiply(double value)
///实现矩阵的乘法
public Matrix Multiply(Matrix other)
///复矩阵的乘法
public bool Multiply(Matrix ar, Matrix ai, Matrix br, Matrix bi, Matrix cr, Matrix ci)
///矩阵的转置
public Matrix Transpose()
///实矩阵求逆的全选主元高斯-约当法
public bool InvertGaussJordan()
///复矩阵求逆的全选主元高斯-约当法
public bool InvertGaussJordan(Matrix mtxImag)
///对称正定矩阵的求逆
public bool InvertSsgj()
///* 托伯利兹矩阵求逆的埃兰特方法
public bool InvertTrench()
///求行列式值的全选主元高斯消去法
public double ComputeDetGauss()
///求矩阵秩的全选主元高斯消去法
public int ComputeRankGauss()
///对称正定矩阵的乔里斯基分解与行列式的求值
public bool ComputeDetCholesky(ref double realDetValue)
///矩阵的三角分解,分解成功后,原矩阵将成为Q矩阵
public bool SplitLU(Matrix mtxL, Matrix mtxU)
///一般实矩阵的QR分解,分解成功后,原矩阵将成为R矩阵
public bool SplitQR(Matrix mtxQ)
/// 一般实矩阵的奇异值分解,分解成功后,原矩阵对角线元素就是矩阵的奇异值
public bool SplitUV(Matrix mtxU, Matrix mtxV, double eps)
///内部函数,由SplitUV函数调用
private void sss(double[] fg, double[] cs)
///求广义逆的奇异值分解法,分解成功后,原矩阵对角线元素就是矩阵的奇异值
public bool InvertUV(Matrix mtxAP, Matrix mtxU, Matrix mtxV, double eps)
///约化对称矩阵为对称三对角阵的豪斯荷尔德变换法
public bool MakeSymTri(Matrix mtxQ, Matrix mtxT, double[] dblB, double[] dblC)
/// 实对称三对角阵的全部特征值与特征向量的计算
public bool ComputeEvSymTri(double[] dblB, double[] dblC, Matrix mtxQ, int nMaxIt, double eps)
///* 求赫申伯格矩阵全部特征值的QR方法
public bool ComputeEvHBerg(double[] dblU, double[] dblV, int nMaxIt, double eps)
/// 求实对称矩阵特征值与特征向量的雅可比法
public bool ComputeEvJacobi(double[] dblEigenValue, Matrix mtxEigenVector, int nMaxIt, double eps)
///求实对称矩阵特征值与特征向量的雅可比过关法
public bool ComputeEvJacobi(double[] dblEigenValue, Matrix mtxEigenVector, double eps)
///雅可比迭代法
public static void Jacobi(Matrix a, Vecter b, out Vecter x)
///根据系数矩阵c和常数项y求解线性方程组
public static int LinearEquations(double[,] c, double[] y, ref double[] x, int unknowNum = 3,int equationNum = 3)
///判断一个浮点数是否等于0
public static bool IsDoubleZero(double v)
///矩阵异常类
public class MatrixException : Exception参考例子:
这是勇哥用excel计算的结果.
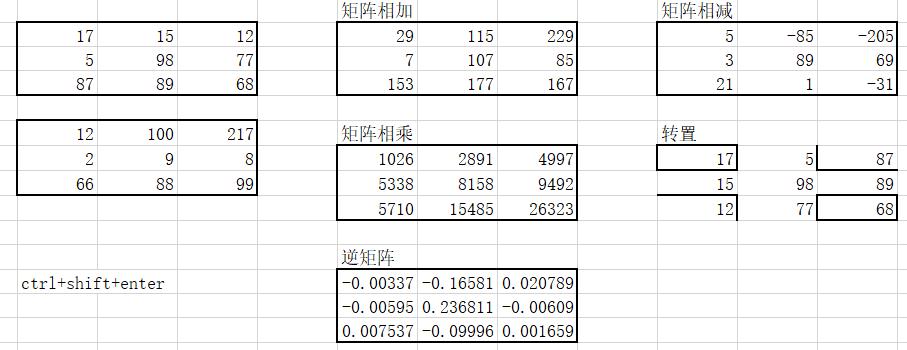
下面用矩阵类演算一遍:
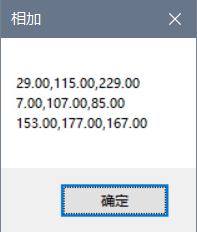
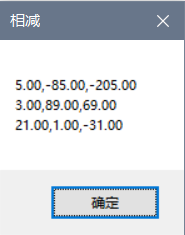
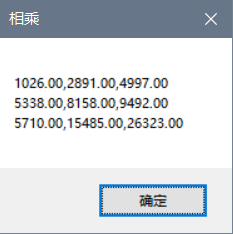
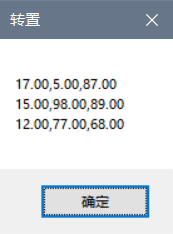
代码如下:
private void button16_Click(object sender, EventArgs e)
{
Matrix matA = new Matrix(new double[3, 3]
{
{17,15,12 },{5,98,77},{87,89,68}
});
Matrix matB = new Matrix(new double[3, 3]
{
{12,100,217 },{2,9,8},{66,88,99}
});
//比较用的精度
matA.SetEps(0.00001);
matB.SetEps(0.00001);
var m1 = matA + matB;
MessageBox.Show(m1.ToString(),"相加");
m1 = matA - matB;
MessageBox.Show(m1.ToString(), "相减");
m1 = matA * matB;
MessageBox.Show(m1.ToString(), "相乘");
m1 = matA.Transpose();
MessageBox.Show(m1.ToString(), "转置");
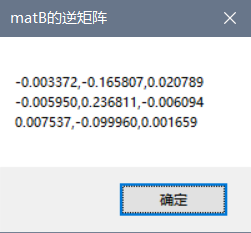
matB.InvertGaussJordan();
MessageBox.Show(matB.ToString(), "matB的逆矩阵");
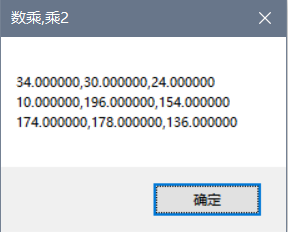
m1 = matA.Multiply(2);
MessageBox.Show(m1.ToString(), "数乘,乘2");
}
---------------------
作者:hackpig
来源:www.skcircle.com
版权声明:本文为博主原创文章,转载请附上博文链接!

 少有人走的路
少有人走的路