勇哥曾经很向往有一台机器人,好在家里搞些视觉实验。
可惜这东西值一台四轮车的钱,估计真买了的话,会被老婆按在地上摩擦。
其实仔细想想,视觉对位的应用,难点在于标定、还有标定后的对位过程,而不在于怎么找线找点(当然有些时候这个也是难点,但是跟物料关系密切,也就是变成了解决工艺上的问题,不存在原理都不懂的的懵逼)
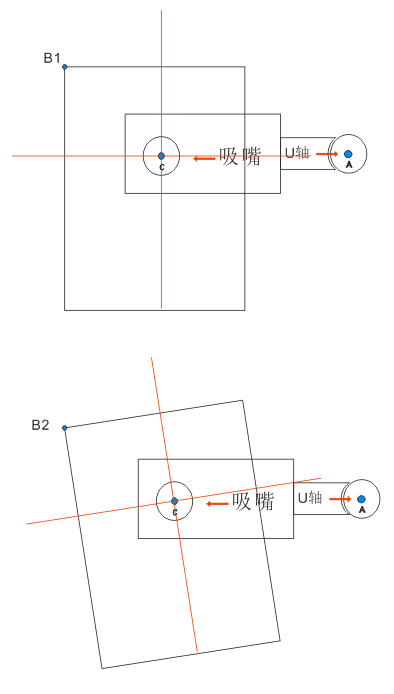
标定的过程主要难点在机器人吸盘的中心和法兰盘的中心不共心,还有些应用中涉及到多相机协调,如果B相机不方便标定,你还得把A相机的标定结果映射过去……
标定后的对位也是困难的地方,这个涉及到参考模板与现在工料位置的比较计算,然后才得到机器人当前的取料坐标,如果是下相机拍照的这种模式,同时物料特征点与机器人的法兰盘中心不共心的话就复杂了,需要多次旋转坐标然后才可以和参考模板进行比对结果,最后计算出放料位置……
好像以上的过程再怎么样,都最好需要一个机器人来验证这些过程。其实不然,勇哥看到过有人用CAD来验证这些过程的原理,也是不错的一种办法。
这里勇哥就边学边卖,试试这个办法。
----------------------------------------------
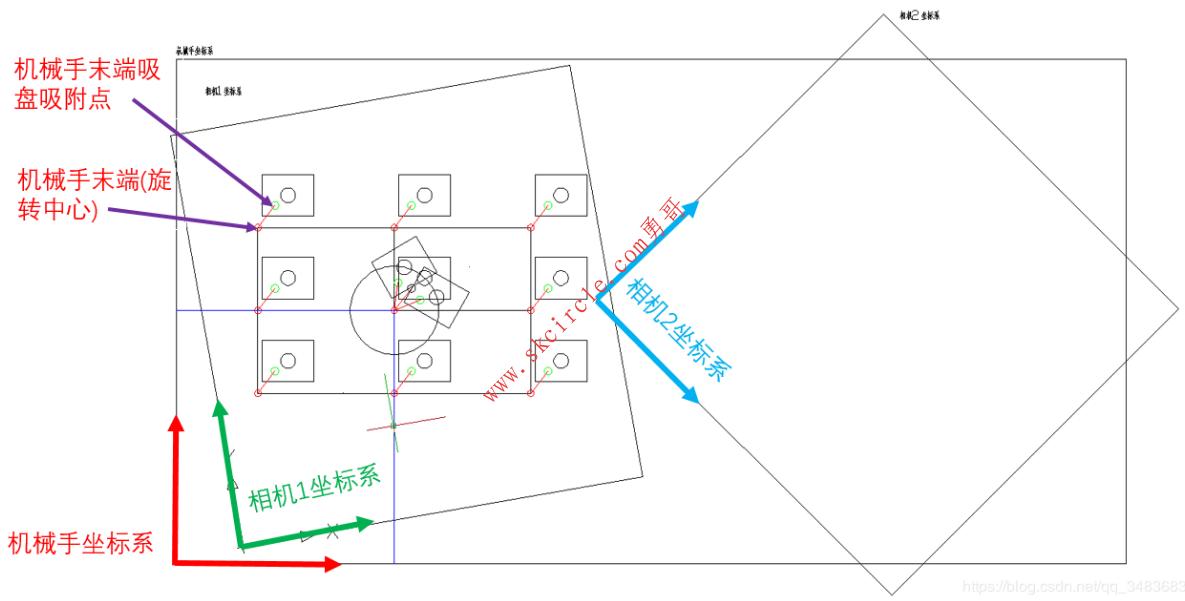
我们先用CAD画三个矩形。
最大的矩形代表机器人的坐标系,内部左边那个是CCDA的坐标系,另一个是CCDB的坐标系。
其中CCDA和CCDB的矩形勇哥画成2560×1920这么大,也就是500W相机的像素矩阵大小。
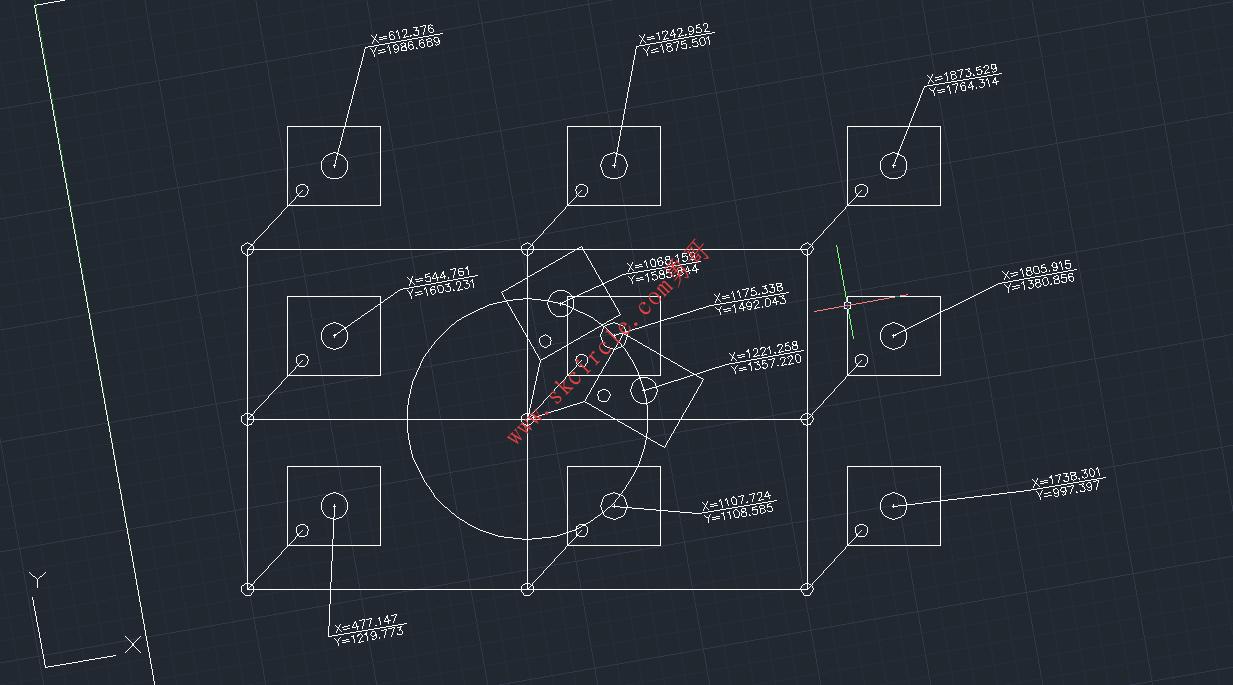
如下图所示。
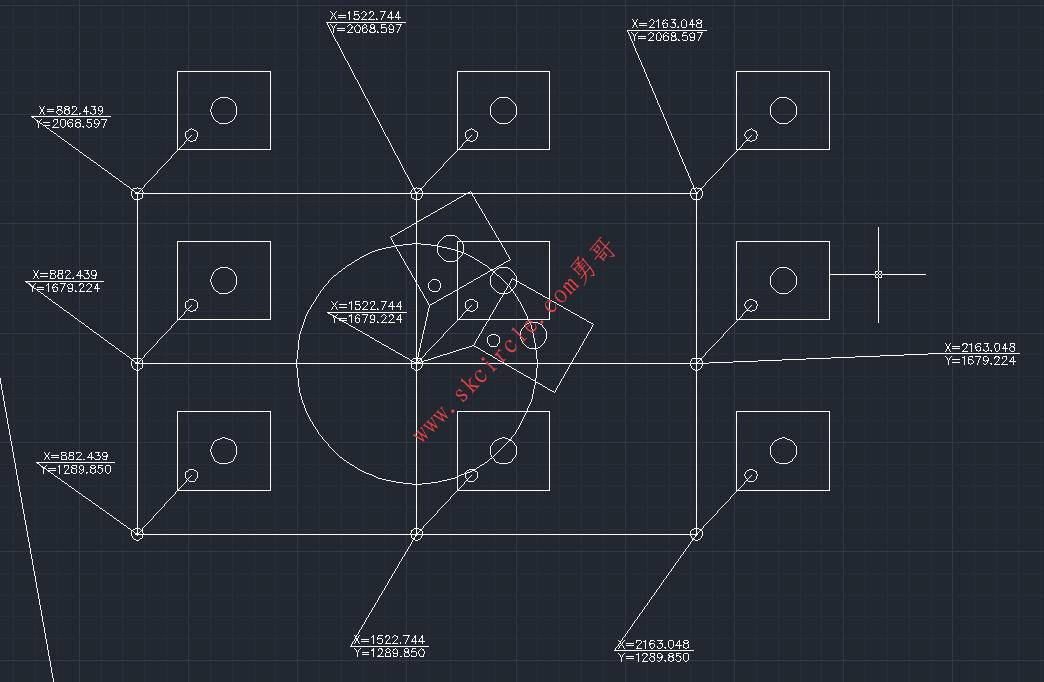
其九点标定位置上标注的黑色圆心是视觉要取得的mark点,绿色圆是机械手未端,即旋转中心。(就是四轴机器人的法兰盘中心)。
下面用cad注释了一下9个点机械坐标
它是机器人未端旋转中心的坐标。
接下来我们应该切换到CCDA的坐标系上去。
如下图所示,CCDA的坐标系,红线所示应该为X轴,蓝线为Y轴。
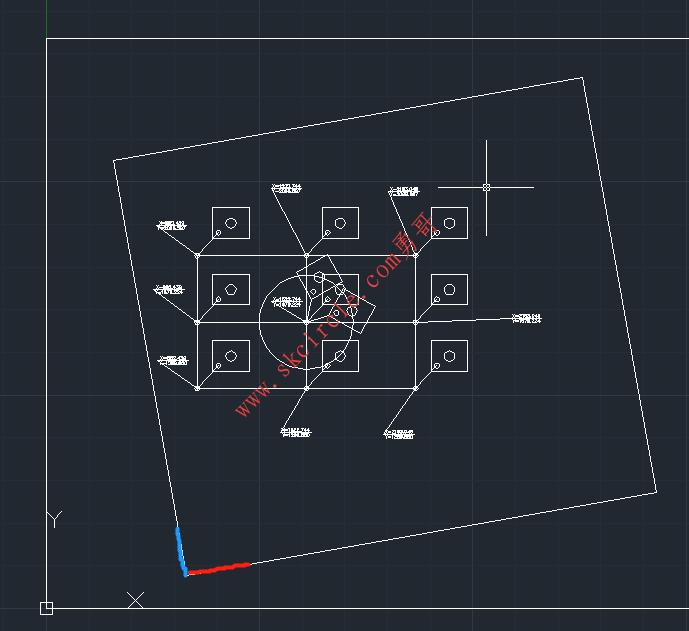
使用ucs指令,ob方式,点击CCDA的矩形
可以看到坐标系统切换成了我们想要的。
注意:如果你的x,y朝向反了,可以再次执行ucs指令,旋转它的x,y,z轴一定角度,直到x,y方向正确为止。
现在取到了CCDA的12点像素坐标(包括了3个旋转点的像素坐标)。
取的是标定片的大圆心的坐标。
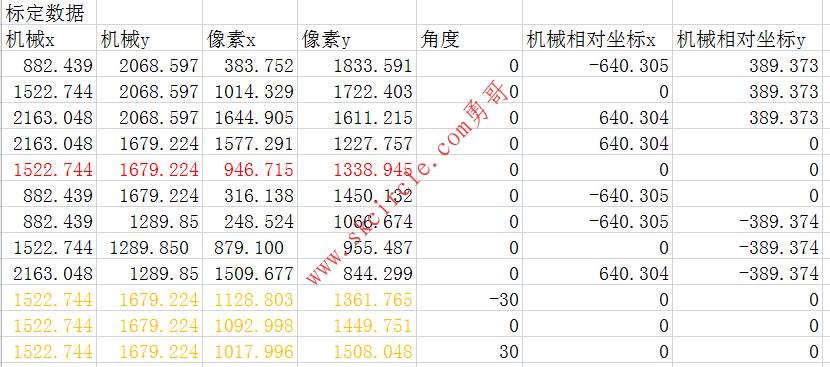
在excel中填表,记录一下我们得到的坐标数据。
注意点的顺序按下面的顺序记录。
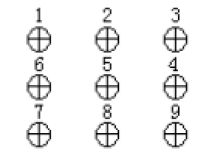
打开visonMaster,用它的N点标定工具做标定。
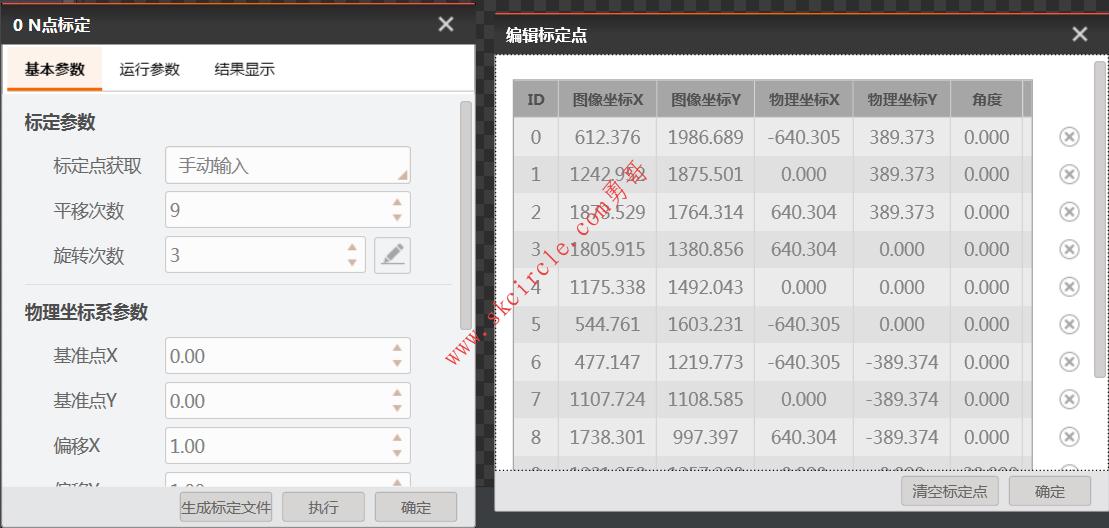
可以看到输完执行之后,像素精度居然是1.0,这是由于点是完全一一对应的,所以标定平移和旋转误差都是0,实际生产中,这里是有标定误差值的。
同时,这边也算出了机械手末端中心在图像中的理论像素坐标(946.714, 1338.944)。
我们回到CAD图中,把图纸的坐标系从机械手坐标系切换到CCDA的坐标系,看看第五点,机械手的旋转中心的像素坐标是多少?
没错就是下图粗红色圆圈出来的地方,查看坐标发现是一致的。

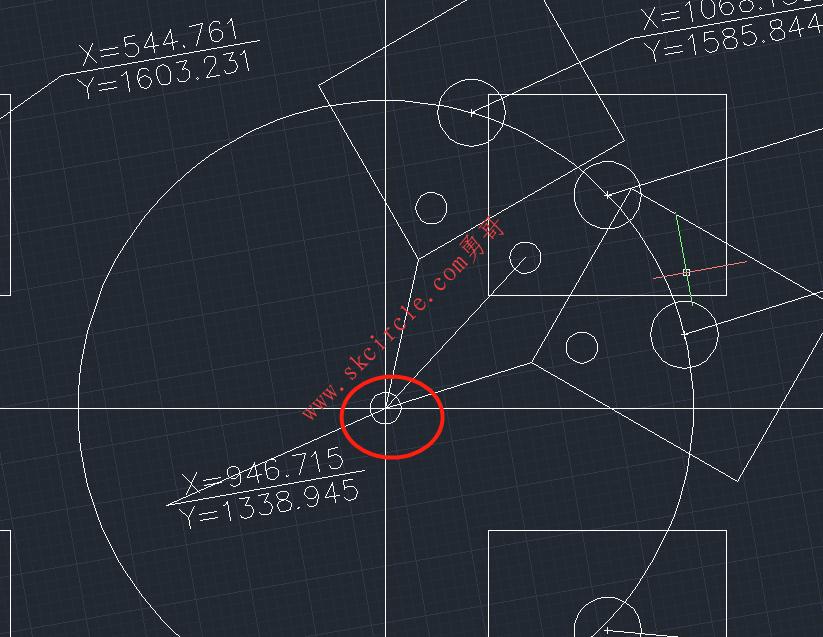
到了这一步,CCDA就已经标定完成了。
再看看VisionMaster的“N点标定”算子的其它参数,算是涨涨见识吧:
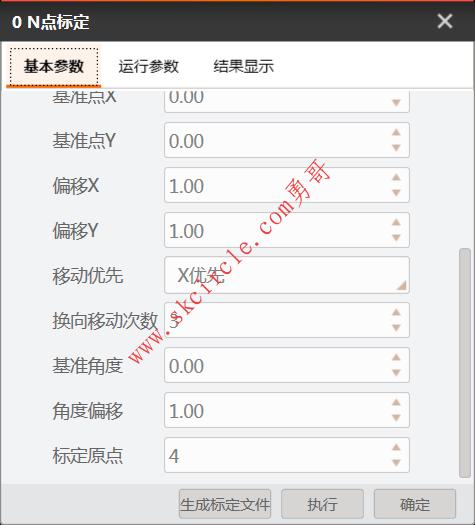
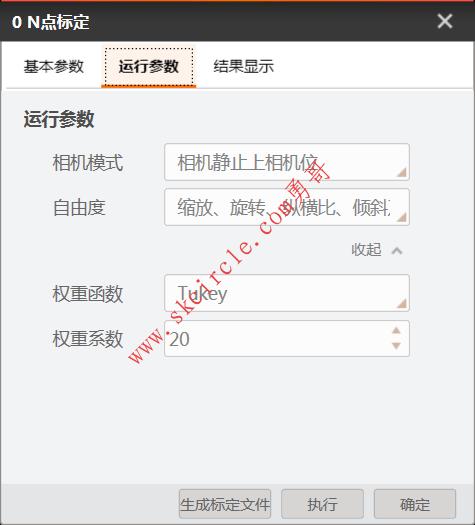
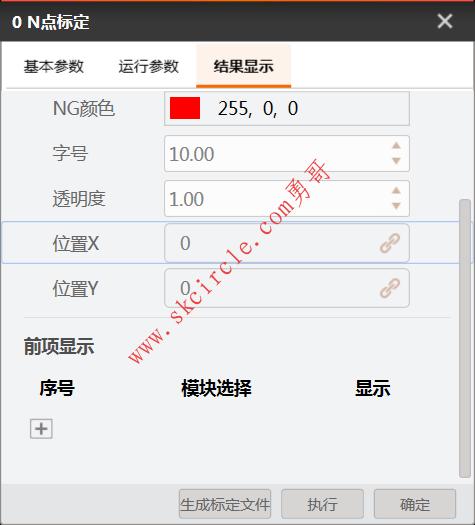
问题来了,怎么用halcon实现VisionMaster的“N点标定”呢?
勇哥重新提供一组数据如下,其中红框处三条是三点旋转的数据。
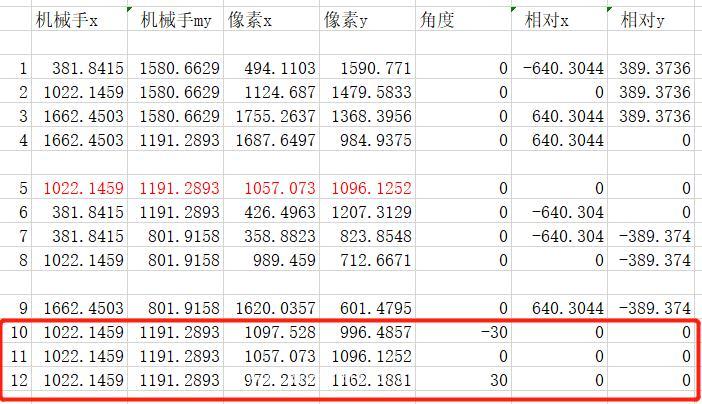
第1到9条数据可以使用halcon的算子vector_to_hom_mat2d来进行标定。
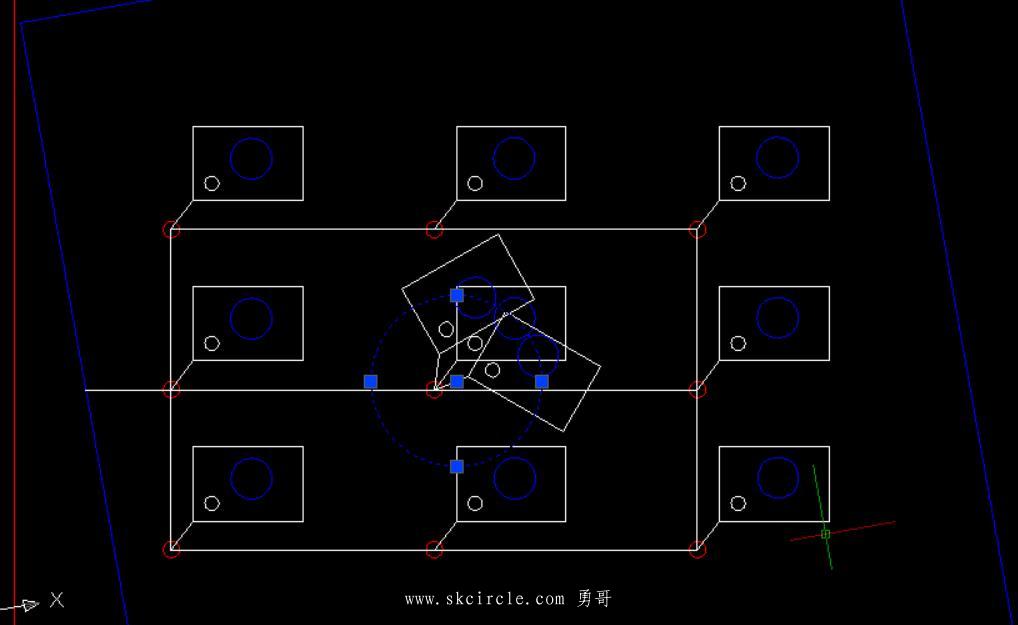
而第10到12的三条数据采用3点定圆的方式取得圆心的信息,在autocad中,也就是画圆的3p方式。
在下图中,过三个圆心的圆是蓝颜色的圆,它的圆心就是我们要求的。其值是x=891.37, y=970.815
附上halcon的实现代码如下:
其中算子hom_mat2d_to_affine_par是检查标定完的矩阵是否精度足够好。
详细可以参考《http://www.skcircle.com/?id=837》
halcon这个验证精度的算子的结果跟visionPro是一样的(如下图),
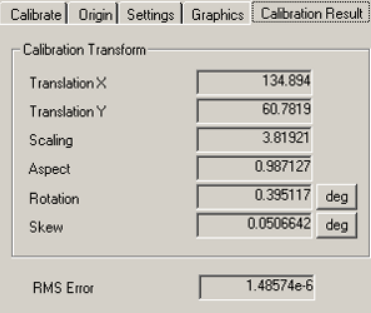
但是和visionMaster不一样(如下图)。

//像素坐标 px:=[494.1103,1124.687,1755.2637,1687.6497,1057.073,426.4963,358.8823,989.459,1620.0357] py:=[1590.771,1479.5833,1368.3956,984.9375,1096.1252,1207.3129,823.8548,712.6671,601.4795] //机械坐标 mx:=[381.8415,1022.1459,1662.4503,1662.4503,1022.1459,381.8415,381.8415,1022.1459,1662.4503] my:=[1580.6629,1580.6629,1580.6629,1191.2893,1191.2893,1191.2893,801.9158,801.9158,801.9158] //标定 vector_to_hom_mat2d (px, py, mx, my, HomMat2D) //sx=1,sy=1,phi=0.174533,theta=1.75614e-09,tx=171.472,ty=-71.7421 hom_mat2d_to_affine_par(HomMat2D, Sx, Sy, Phi, Theta, Tx, Ty) //计算机械手末端中心在图像中的理论像素坐标 rx:=[1097.528,1057.073,972.2182] ry:=[996.4857,1096.1252,1162.1881] x1:= rx[0] x2:= rx[1] x3:= rx[2] y1:= ry[0] y2:= ry[1] y3:= ry[2] a:=x1 - x2 b:= y1 - y2 c:= x1 - x3 d:= y1 - y3 e:= ((x1 * x1 - x2 * x2) + (y1 * y1 - y2 * y2)) / 2.0 f:= ((x1 * x1 - x3 * x3) + (y1 * y1 - y3 * y3)) / 2.0 det:= b * c - a * d radius:=0 if(fabs(det) < 1e-5) radius:= -1 else //x0=891.37, y0=970.815 x0:= -(d * e - b * f) / det y0:= -(a * f - c * e) / det tuple_sqrt(a*a+b*b, radius) endif
---------------------
作者:hackpig
来源:www.skcircle.com
版权声明:本文为博主原创文章,转载请附上博文链接!

 少有人走的路
少有人走的路