少有人走的路本文介绍的Matrix，是.net自带的类. 其命名空间为：System.Drawing.Drawing2D
注意并不是netMarketing中那个netMarketing.graphics.Matrix
在GDI+中，可以在Matrix对象中存储仿射变换。由于表示仿射变换的矩阵的第三列总是（0,0,1），因此在构造Matrix对象时，只需要指定前两列的6个数。语句：
Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4)
构造下面图形中显示的矩阵。
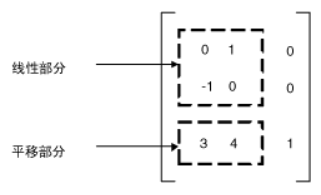
Matrix 由默认构造函数构造的默认矩阵的值为（1,0,0,1,0,0）。在矩阵表示为:
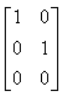这是对以下内容的简化：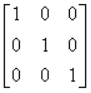
这是因为由于表示仿射变换的矩阵的第三列总是（0,0,1）
Matrix 类提供了四个变换运算: 分别是旋转，位移，绽放，斜切：
RotateTranslateScaleShear
上面的变换也可以自由组合，形成复合变换．
下面勇哥来演示一下常见的变换指令的用法.
//变换之前的三个点 points[0] = new Point(30, 20); points[1] = new Point(100, 40); points[2] = new Point(100, 80);
(1)旋转
1.1 以原点旋转
//以原点0,0旋转 var m = new System.Drawing.Drawing2D.Matrix(); m.Rotate(45); //也可以用m.RotateAt(45,new PointF(0, 0); 结果是一样的. m.TransformPoints(points); draw(points);
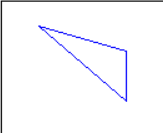
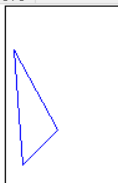
Rotate执行之后矩阵值为:
m.Elements
{float[6]}
[0]: 0.707106769
[1]: 0.7071067
[2]: -0.7071067
[3]: 0.707106769
[4]: 0
[5]: 0由上述值可见, 旋转矩阵的原型为:
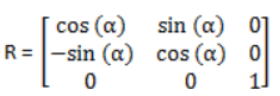
应用上面的矩阵,变换后的三个点坐标为:
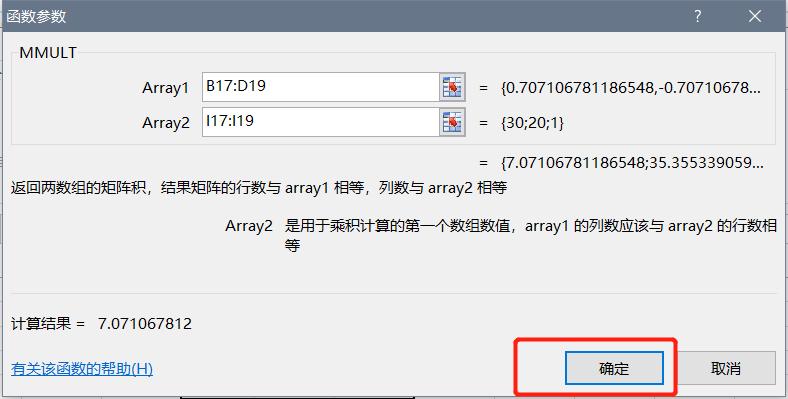
勇哥用excel验算一下:
可见结果是一致的.
注意在excel中, 你应该按下面的顺序排列矩阵元素, 否则算出来的x,y做次序颠倒.
cos(a), -sin(a)
sin(a), cos(a)
另外, 矩阵的乘法不是用符号*, 而是应该用函数MMULT
这个函数填写完参数后, 要按ctrl+shift+Enter, 而不是直接确定.
1.2 以指点定旋转
//顺时针转45度，由点points[0] var m = new System.Drawing.Drawing2D.Matrix(); m.RotateAt(45, new PointF(points[0].X, points[0].Y)); m.TransformPoints(points); draw(points);
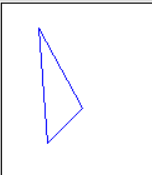
旋转之后矩阵值为:
m.Elements
{float[6]}
[0]: 0.707106769
[1]: 0.7071067
[2]: -0.7071067
[3]: 0.707106769
[4]: 22.92893
[5]: -15.3553391在上面的矩阵中, 看到平移数据 22.92893, -15.3553391
这个是怎么来的? 勇哥猜测是复合变换而来的.
关于这一点, 请看本文结尾处的实验验证.
应用上面的矩阵,变换后的三个点坐标为:
(2)缩放
//x,y缩放2倍 var m = new System.Drawing.Drawing2D.Matrix(); m.Scale(2, 2); m.TransformPoints(points); draw(points);
scale后的矩阵的元素为:
m.Elements
{float[6]}
[0]: 2
[1]: 0
[2]: 0
[3]: 2
[4]: 0
[5]: 0由这个我们可以知道缩放矩阵的原型:
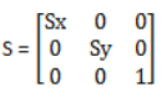
下面是用上面的矩阵计算出来的坐标:
勇哥用excel验算一下:
可见结果是一致的.
(3)平移
//位移 var m = new System.Drawing.Drawing2D.Matrix(); m.Translate(100, 50, System.Drawing.Drawing2D.MatrixOrder.Append); m.TransformPoints(points); draw(points);
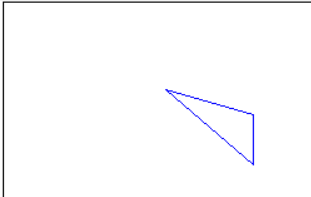
Translate执行后矩阵内容如下:
m.Elements
{float[6]}
[0]: 1
[1]: 0
[2]: 0
[3]: 1
[4]: 100
[5]: 50由此可见平移矩阵的原型如下:
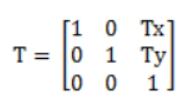
由上面矩阵计算出来的点位如下:
用excel验证一下:
结果是一致的.
(4)斜切
//斜切 var m = new System.Drawing.Drawing2D.Matrix(); m.Shear(1.5f, 0); m.TransformPoints(points); draw(points);
m.Elements
{float[6]}
[0]: 1
[1]: 0
[2]: 1.5
[3]: 1
[4]: 0
[5]: 0由上面结果可知斜切矩阵原形为:
1, 1.5, 0
0, 1 ,0
0, 0 ,1
由上面矩阵求出的点位为:
用excel验证一下:
结果是一致的.
(5) 镜像
Matrix没有镜像的指令.
勇哥直接说说镜像的矩阵:
沿X轴镜像的矩阵是:（1,0,0，-1,0,0）。沿Y轴镜像矩阵为（-1,0,0,1,0,0）
//沿x镜像 var m = new System.Drawing.Drawing2D.Matrix(1,0,0,-1,0,0); m.TransformPoints(points); draw(points);
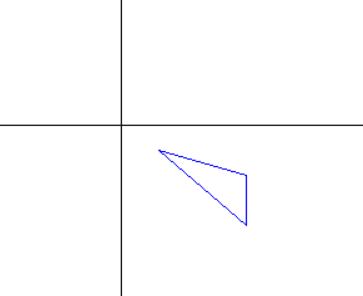
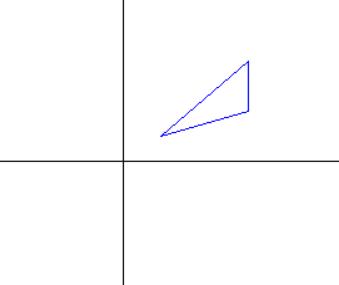
//沿y镜像 var m = new System.Drawing.Drawing2D.Matrix(-1, 0, 0, 1, 0, 0); m.TransformPoints(points); draw(points);
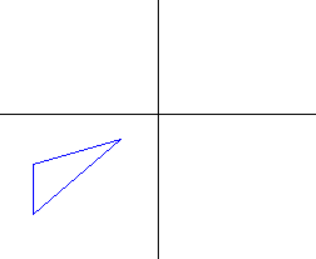
(6)复合变换
//复合变换 var m = new System.Drawing.Drawing2D.Matrix(); m.RotateAt(65, new PointF(points[0].X, points[0].Y)); m.Scale(2, 2, System.Drawing.Drawing2D.MatrixOrder.Append); m.Translate(100, 50, System.Drawing.Drawing2D.MatrixOrder.Append); m.TransformPoints(points); draw(points);
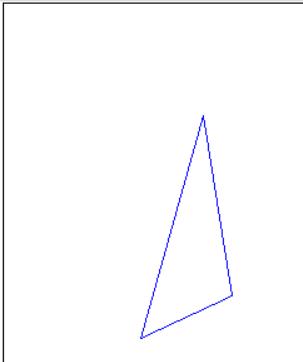
下面是复合变换后矩阵的元素值:
分别为: Matrix缺省, 旋转, 缩放, 平移
m.Elements
{float[6]}
[0]: 1
[1]: 0
[2]: 0
[3]: 1
[4]: 0
[5]: 0
m.Elements
{float[6]}
[0]: 0.42261833
[1]: 0.9063077
[2]: -0.9063077
[3]: 0.42261833
[4]: 35.4476
[5]: -15.6416016
m.Elements
{float[6]}
[0]: 0.845236659
[1]: 1.81261539
[2]: -1.81261539
[3]: 0.845236659
[4]: 70.8952
[5]: -31.2832031
m.Elements
{float[6]}
[0]: 0.845236659
[1]: 1.81261539
[2]: -1.81261539
[3]: 0.845236659
[4]: 170.8952
[5]: 18.7167969复合变换是一个接一个的变换序列，看看下面列表中的矩阵和变换（矩阵的本质是其所在空间的一种跃迁（变换））：
| 矩阵A | 旋转90度 |
| 矩阵B | 在x方向上缩放2倍 |
| 矩阵C | 在y方向上平移3个单位 |
在仿射空间中，如果从由矩阵[2 1 1]表示的点(2,1)开始，先后乘以A、B、C，在点(2,1)将按列出的顺序经历三种变换。
[2 1 1]ABC = [-2 5 1]
可以不将复合变换的三部分存储于三个独立的矩阵，而是一起乘以A、B和C来得到存储整个复合变换的单个的3x3矩阵。假定ABC=D，则一个点乘以D得出的结果与一个点先后乘以A、B、C的结果相同。
[2 1 1]D = [-2 5 1]
下图显示了矩阵A、B、C和D
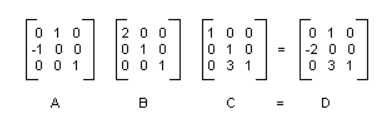
复合变换的矩阵可以通过将几个单独的变换矩阵相乘而得到，这就意味着任何仿射变换的序列均可存储于单个的Matrix对象中。
注意：复合变换的顺序非常的重要。一般来说，先旋转、在缩放、然后平移，与先缩放、再旋转、然后平移是不同的。同样，矩阵相乘的顺序也是重要的。这就对应着矩阵ABC与BAC一般不同。
对于复合变换的顺序问题, 勇哥举一个例子:
1.2 以指点定旋转的例子中, RotateAt指令后, 矩阵的结果为:
m.Elements
{float[6]}
[0]: 0.707106769
[1]: 0.7071067
[2]: -0.7071067
[3]: 0.707106769
[4]: 22.92893
[5]: -15.3553391其中看到平移数据 22.92893, -15.3553391
这个是怎么来的? 勇哥当时猜测是复合变换而来的.
复合变换的过程如下:
先把第一个点(30,20)移动到原点
再沿原点旋转45度
再把结果移动回原来的(30,20)位置
错误的代码如下:
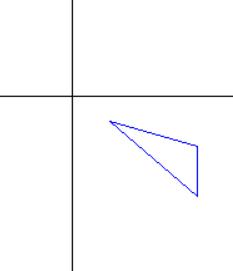
var m = new System.Drawing.Drawing2D.Matrix(); m.Translate(-30, -20); m.Rotate(45); m.Translate(30, 20); m.TransformPoints(points); draw(points);
这个代码和上面说的变换过程是一致的, 但是结果却是不对的.
而且有意思的是, 经过上面的变换, 矩阵为:
m.Elements
{float[6]}
[0]: 0.707106769
[1]: 0.7071067
[2]: -0.7071067
[3]: 0.707106769
[4]: -22.9289341
[5]: 15.3553314这个结果还是对的, 但是应用它到每个点的结果却是不对的
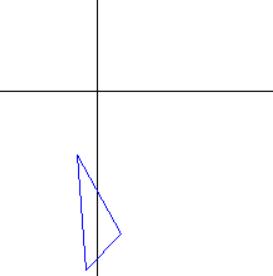
正确的代码如下:
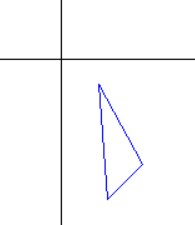
//复合变换实现RotateAt的效果 //(30, 20);(100, 40);(100, 80); var m = new System.Drawing.Drawing2D.Matrix(); m.Translate(30, 20); m.Rotate(45); m.Translate(-30, -20); m.TransformPoints(points); draw(points);
正确的写法其实是把上面说的复合变换过程反过来写.
这个例子充分说明了矩阵的乘法不满足交换率, 先做什么再做什么, 次序十分关键.
MatrixOrder.Append和MatrixOrder.Prepend的作用
勇哥还是想杠一下, 正确的代码的书写顺序不符合逻辑顺序, 不直观呀!
对于这个问题, Matrix类在变换函数里面都引入了一个MatrixOrder枚举变量
这两个枚举官方解释是:
Append是在旧操作后应用新操作。
Prepend在旧操作前应用新操作。
官方解释不是太好明白, 由上面勇哥举的例子, Append可理解为从后往前计算, 而Prepend可理解为由上到下顺序计算.
所以代码可以改成下面这样, 这样即符合了逻辑顺序, 结果也是正确的.
var m = new System.Drawing.Drawing2D.Matrix(); m.Translate(-30, -20,System.Drawing.Drawing2D.MatrixOrder.Append); m.Rotate(45, System.Drawing.Drawing2D.MatrixOrder.Append); m.Translate(30, 20, System.Drawing.Drawing2D.MatrixOrder.Append); m.TransformPoints(points); draw(points);
---------------------
作者：hackpig
来源：www.skcircle.com
版权声明：本文为博主原创文章，转载请附上博文链接！
