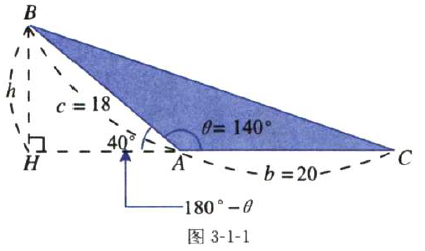
少有人走的路见下图，求三角形ΔABC的面积。
按三角形面积公式 
（面积=底×高÷2。其中，a是三角形的底，h是底所对应的高）
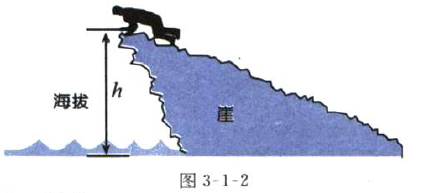
设底边b=20，经过顶点B作底边CA的垂直线，则点H就会落在CA的延长线上，BH就是三角形的高h，这和图3-1-2测量海拔高度是一样的。
在做高h时，我们创建了一个三角形Δ
由于h/c=sin40° ，得h=c*sin40°
∴ SΔABC= 1/2*b*h
=1/2*20*18*sin40°
通过上述推导，说明了钝角的三角函数是如何求取。（求补角的方式）
其实同时也推导出了已知道两边和一个角怎么求三角形面积。
通常，我们把θ的补角写作180°-θ，然后就得出以下三组诱导公式：
也就是说，互为补角的两个角的sin值相等，cos和tan互为相反数。
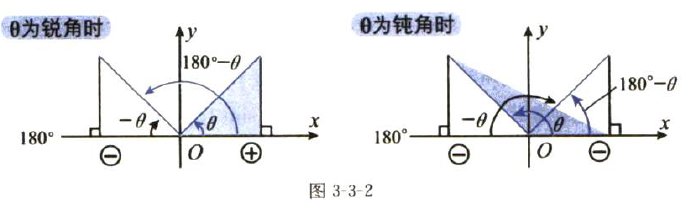
图3-3-2中的阴影部分表示θ。从中也能看出y始终大于等于零，即y≥0。
当θ≥90°时，可以通过上面的诱导公式把θ转换为90°以内的锐角来计算。
下面来讨论三角形面积公式
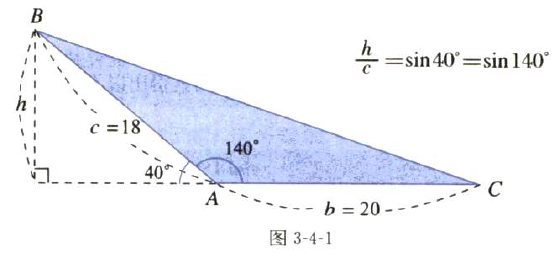
图3-4-1中，如果用两边与它们的夹角来求面积的话，公式是：
S=1/2*b*c*sinA （1）
当∠A＝90°时，ΔABC就成了直角三角形，底边b上的高就是c了。
∴ S＝1/2*b*c
如果直接把A＝90°(sin90°=1)代入式子（1）中，就会得出和直角三角形面积公式一样的式子：
S=1/2*b*c*sinA＝1/2*b*c*sin90°＝1/2*b*c
有些书中，三角形的面积通常都是下面几种形式：
S=1/2(bc).sinA
=1/2(ca).sinB
=1/2(ab).sinC
这三个公式只是用于不同的内角而显得有所不两只而已，其实是一回事。
它们中每一组都有两个小写字母（即两条边）和一个大写字母（即它们的夹角），并且同一组合中不能有两个相同的字母。换句话说，这是两条边和它们的夹角的组合。
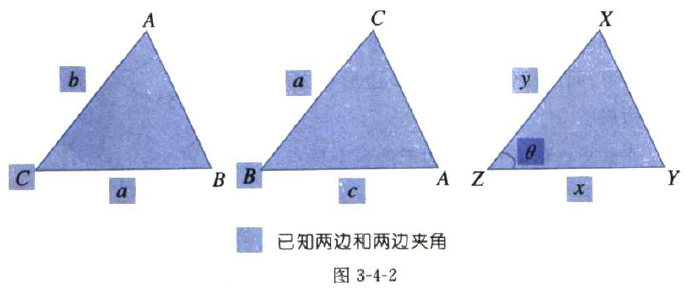
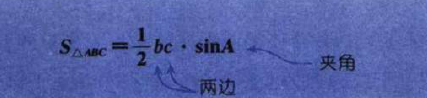
如图3-4-2(3)所示，在ΔXYZ中，已知两边x,y和它们夹角Z（用θ表示)，则三角形的面积就是：
S=1/2(xy).sinθ
总结一下三角形的面积公式：
S=1/2*(两边的积)*sin(夹角)
例子： 求半径为1的圆的内接正七十二边形的面积，结果保留两位小数。
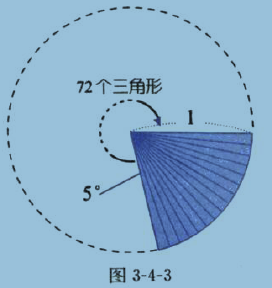
连接圆心和正七十二边形的各个顶点，就会得到72个顶角为360/72=5°、腰为1（圆半径）的等腰三角形。
1/2*1*1*sin5°*72≈0.0871557427*36
＝3.13760
≈3.14
这是因为按圆的面积公式： 
半径为1的圆的面积就是pi
勇哥上一段halcon代码，演示了当正多边形边数足够大时，就会接近圆形。
dev_close_window() dev_open_window(0, 0, 612, 612, 'black', WindowHandle) px:=280 py:=300 r:=200 xary:=[] yary:=[] step:=6 for Index := 0 to 360/step by step x:=px+px/2*cos(rad(step*Index+step)) y:=py+py/2*sin(rad(step*Index+step)) xary[Index/step]:=x yary[Index/step]:=y disp_polygon(200000, xary, yary) endfor
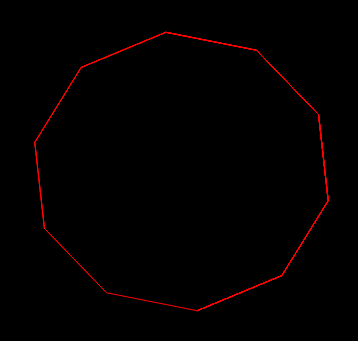
这是step＝6的时候
这是step＝1的时候
其实上面的程序，勇哥想搞成画三角形，然而用算子disp_polygon画三角真是麻烦。
就这样吧。
---------------------
作者：hackpig
来源：www.skcircle.com
版权声明：本文为博主原创文章，转载请附上博文链接！
