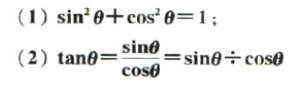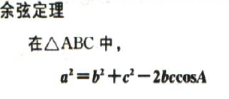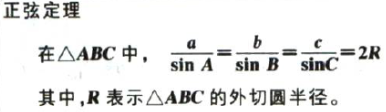少有人走的路

机器视觉常见的数学公式很多，下面的贴子会由浅到深依次跟贴下去，以方便大家查阅与记忆。

（一）　6个必须有记住的三角函数公式：

（二）直线方程相关

（1） 直线斜率

 经过两点P₁(x₁,y₁), P₂(x₂,y₂) (x₁≠x₂)的直线斜率的公式：

（2）两点之间的距离 

平面坐标

空间坐标

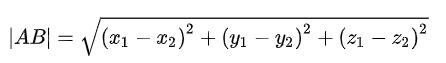
（3）两点式直线方程

（4）直线的一般方程

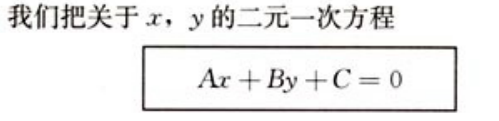
（5）两直线交点

例题：

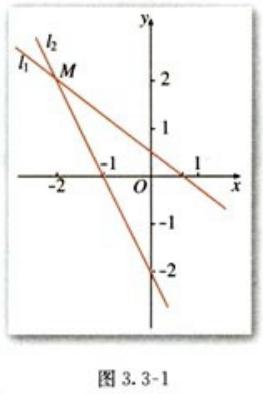
（6）点到直线的距离 

例题：

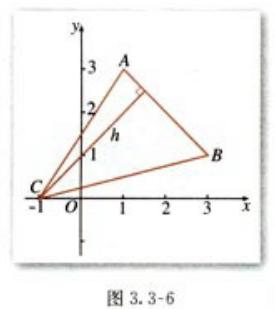
（7）两条平行线间的距离 

（三）圆的方程

(1)圆的标准方程

圆心位置与半径大小确定后，圆就唯一确定了。因此确定一个圆最基本要素是圆心和半径。

如图4.1-1，在直角坐标系中，圆心A的位置用坐标(a,b)表示，半径r的大小等于圆上任意点M(x,y)与圆心A(a,b)的距离，圆心为A的圆就是集合。

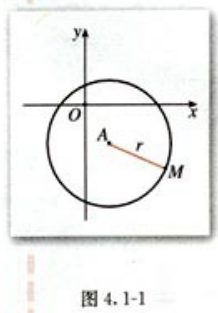
由两点距离公式，点M的坐标适合的条件可以表示为：

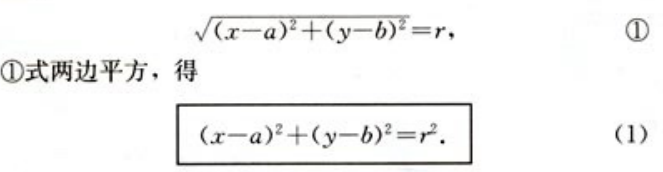
若点M(x,y)在圆上，由上述讨论可知，点M的坐标适合方程（1）；反之，若点M(x,y)的坐标适合方程(1)，这就说明点M与圆心A的距离为r，即点M在圆心为A的圆上。我们把方程（1）称为圆心为A（a,b)，半径为r的圆的方程，把它叫圆的标准方程。

（2）圆的一般方程

例子1：

例子2：

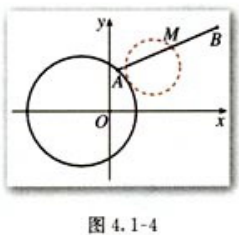
（四）直线与圆的位置关系

由平面几何知,直线与圆有三种位置关系:

（1）直线与圆相交,有两个公共点;

（2）直线与圆相切,只有一个公共点;

（3）直线与圆相离,没有公共点.

判断直线L与圆C的位置关系有两种方法: 

一种方法是判断直线L与圆C的方程组成的方程组是否有解.如果有解,直线L与圆C有公共点. 

有两组实数解时,直线L与圆C相交;

有一组实数解时,直线L与圆C相切;

无实数解时,直线L与圆C相离．

另一种方法是,判断圆C的圆心到直线L的距离d与圆的半径r的关系．

如果d<r,直线1与圆C相交;

如果d=r,直线1与圆C相切;

如果d>r,直线1与圆C相离.

例子：

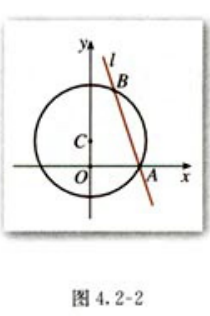
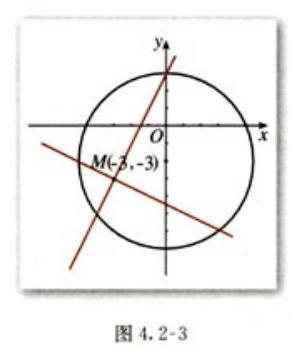
（五）点绕原点旋转

第一种方法：

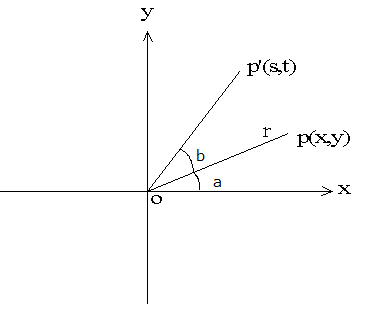
如图，线长OP=OP'=r，点（x,y）以圆点O为旋转中心，逆时针转了b°，求P'(s,t)？

解：  s= r*cos(a+b)

        t= r*sin(a+b)

        x=r*cos(a)

        y=r*sin(a)

第二种方法：

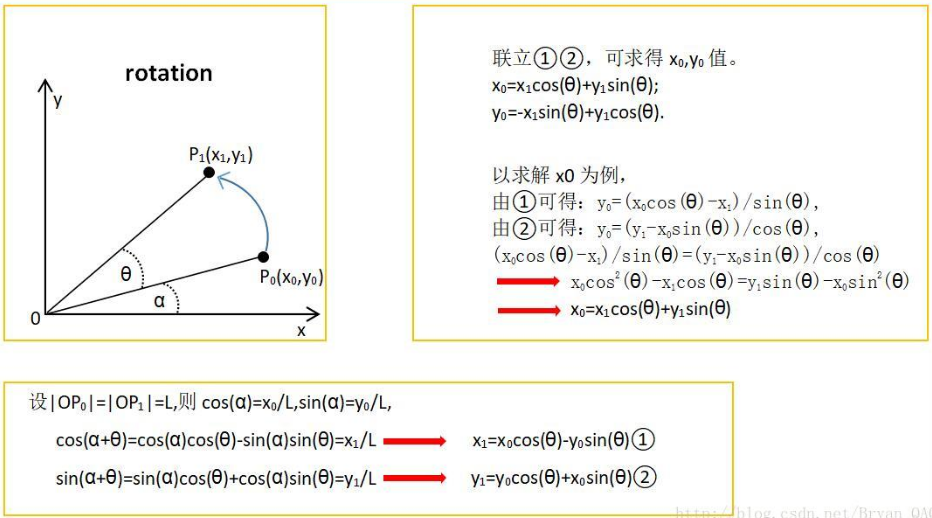
x1=x0cos(θ)-y0sin(θ)
y1=y0cos(θ)+x0sin(θ)

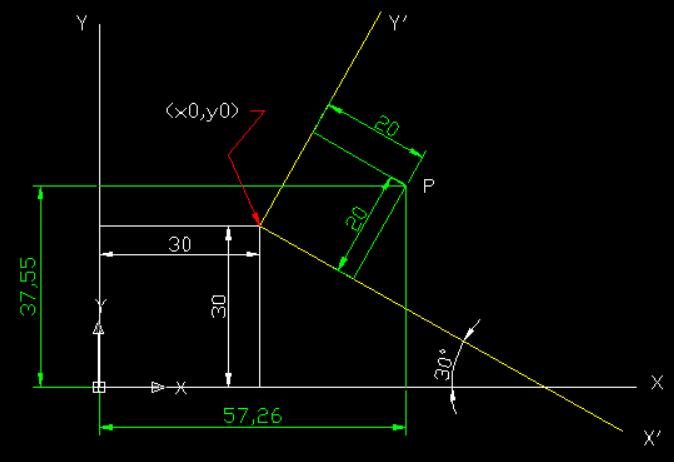
（六）绕任意点旋转

公式是：

x0=cos(a)*(x-rx0)-sin(a)*(y-ry0)+rx0
y0=cos(a)*(y-ry0)+sin(a)*(x-rx0)+ry0

点（x,y) 绕指定点（rx0,ry0)旋转a度后到（x0,y0)， 求x0,y0？

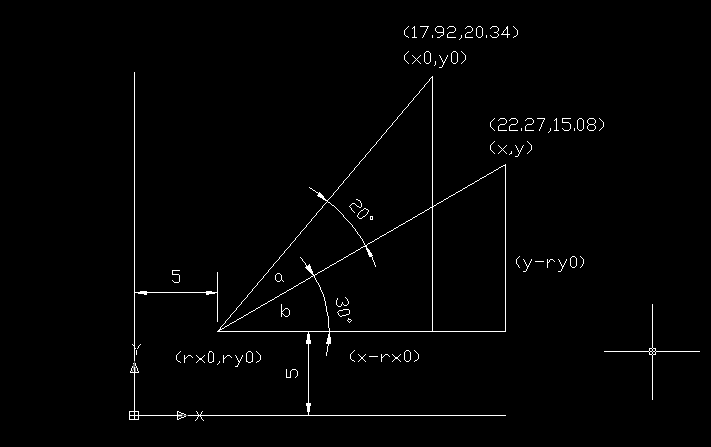
（七）求矩形的四个角点位置

a:= -Length1*Cos - Length2*Sin
b:= -Length1*Sin + Length2*Cos

--------------------- 

作者：hackpig
来源：www.skcircle.com
版权声明：本文为博主原创文章，转载请附上博文链接！

本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：