少有人走的路

命名空间：

netMarketing.MathAnalysis.Vecter

netMarketing.MathAnalysis.Vector3

功能：Vecter类是平面向量类；Vector3是空间向量类（三维向量）

功能详细说明：

Vecter类是矩阵运算类Matrix的基础。对于常见的平面向量计算运算符已经重载。

注意这个类的名字之所以不叫Vector是因为跟某些关键字有重复的原因。

Vector3类是空间向量计算类，空间向量在图形学中应用广泛。例如点乘用于判断向量夹角、计算反射reflect，叉乘用于计算法向量等。

有关空间向量的知识贴见：

向量相关知识见下面贴子：

几何向量(5)：绘制圆计算π  

几何向量(4)：直线和平面   

几何向量(3)：向量乘法（叉乘）  

几何向量(2)：向量乘法（点乘）  

几何向量(1)：基本概念   

平面向量知识整理 　

空间向量知识点归纳总结(经典)

常用函数列表：

Vecter类：
  *    =    -----------向量相等
        *                    注意该方法不需要自行编写重载函数，
        *                    c#已经实现了对类的等号算符重载，并禁止
        *                    用户编写等号算符（=）重载函数
        *    +    -----------两向量对应元素相加
        *    -    -----------两向量对应元素相减
        *    *    -----------两向量对应元素相乘（相当于MATLAB中的  .*算符）
        *    /    -----------两向量对应元素相除（相当于MATLAB中的  ./算符）
        *
        *    +  -----------重载向量加一实数（所有元素）
        *    -  -----------重载向量减一实数（所有元素）
        *    *  -----------重载向量乘一实数（所有元素）
        *    /  -----------重载向量除一实数（所有元素）
        *
        *    +  -----------重载实数加向量（所有元素）
        *    -  -----------重载实数减向量（所有元素）
        *    *  -----------重载实数乘以向量（所有元素）
        *    /  -----------<无>--不重载--<即不能用实数除以向量>
        *
        *    |  （VEC1|ve2）----向量内积
        *    ~  （~VEC1）-------向量2范数，相当于MATLAB中的norm()函数

        
        
Vector3类：                

+，-，*
Cross 差乘
Dot 点乘（点积）
Zero()   置(0,0,0)
One()  置(1,1,1)

参考例子：

(1) 平面向量 和

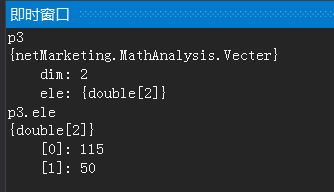
  Vecter p1 = new Vecter(2);
  p1.ele[0] = 35; p1.ele[1] = 35;
  Vecter p2 = new Vecter(2);
  p2.ele[0] = 80; p2.ele[1] = 15;
  var p3 = p1 + p2;

结果：p3(115,50)

（2）平面向量 点乘

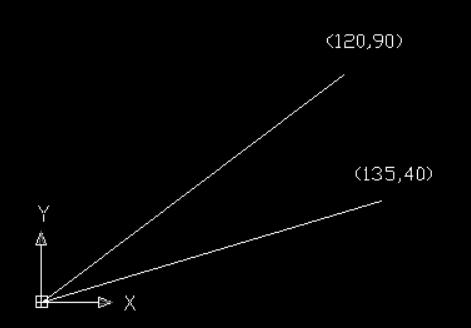
  Vecter p1 = new Vecter(2);
  Vecter p2 = new Vecter(2);
  p1.ele[0] = 120;p1.ele[1] = 90;
  p2.ele[0] = 135; p2.ele[1] = 40;
  var res = p1 | p2;
  //结果：19800

验算一下：

点积＝120*135+90*40=19800

可见是正确的。

（3）空间向量 点乘

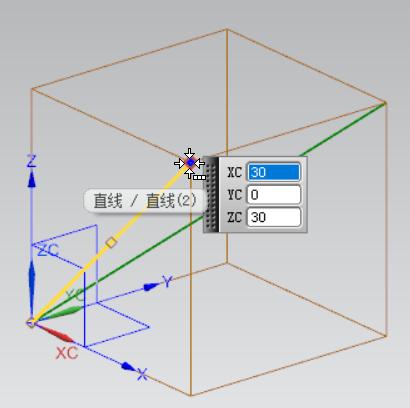
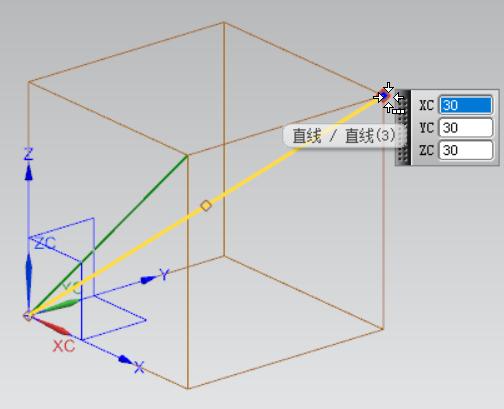
  Vector3 A = new Vector3(30, 0, 30);
  Vector3 B = new Vector3(30, 30, 30);
  var res2 = A.Dot(B);
  //结果：1800

我们验算一下：

>> 表达式: 30*30+0*30+30*30=1800

可以看到是正确的。

（4）空间向量 叉乘

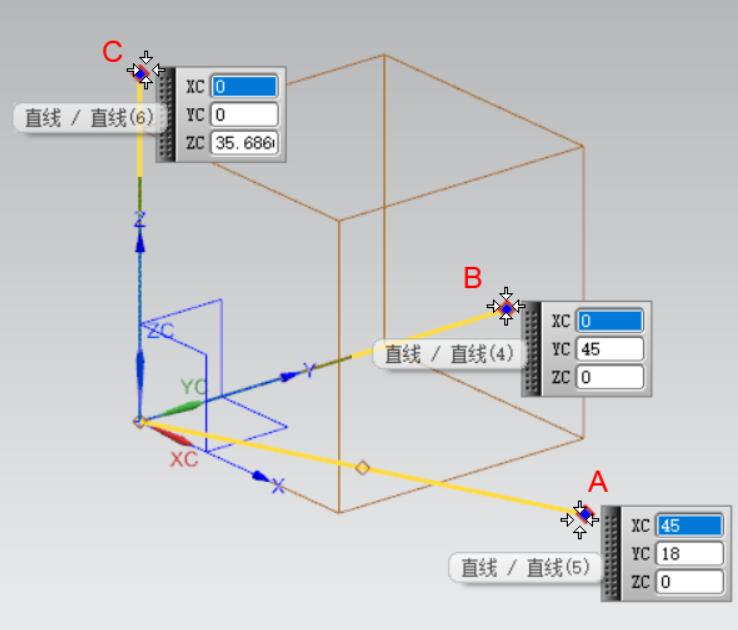
Vector3 A = new Vector3(45, 18, 0);
Vector3 B = new Vector3(0, 45, 0);
var res2 = A.Cross(B);
//结果：(0,0,2025)

验算一下：

(A.y*B.z-A.z*B.y, A.z*B.x-A.x*B.z, A.x*B.y-A.y*B.x)=(0,0,2025)

结果是正确的。

--------------------- 

作者：hackpig
来源：www.skcircle.com
版权声明：本文为博主原创文章，转载请附上博文链接！

返回类库功能说明目录

本文出自勇哥的网站《少有人走的路》wwww.skcircle.com，转载请注明出处！讨论可扫码加群：