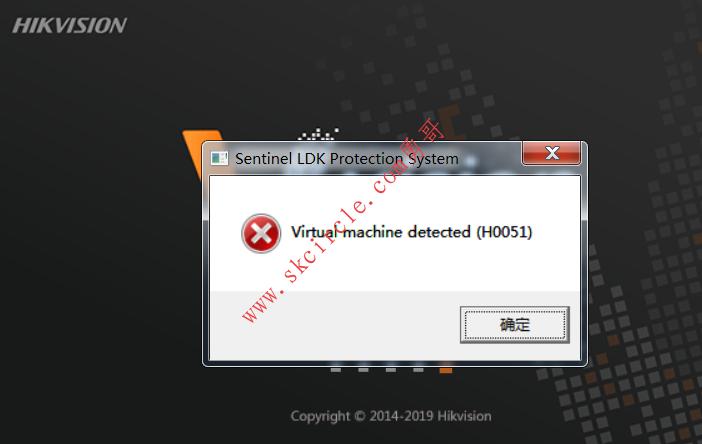
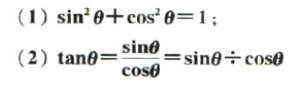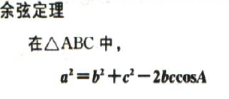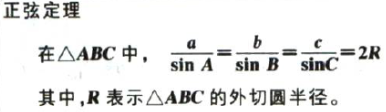直接写出加法定理：
可见，sin(a+b)并不简单等于sina+sinb。
之前说过，在三角函数中我们只需要掌握6个公式（其它的做到可以推理出来），加上这两个，就齐全了。
而tan的加法定理可以通过tanθ=sinθ/cosθ推导出来。
tan(a+β)= sin(a+β)/cos(a+β)
=(sinacosβ+cosasinβ)/(cosacosβ-sinasinβ)
这个等式右边也用tan来表示的话，就要把等式右边的分子分母都同时除以cosacosβ，
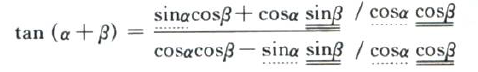
虚线处是tana，双下划线处是tanβ，而没有记号的地方被约分为1，
这样我们就推导出tan的加法定理，
tan(a+β)=(tana+tanβ)/(1-tanatanβ)
同理：
tan(a-β)=(tana-tanβ)/(1-tanatanβ)
最后我们回忆一下6个必须有记住的三角函数公式：
√ ∠ θ α β ° Δ
≥ ≤ ≈ ≠
∵ 因为
∴ 所以
ι π
120