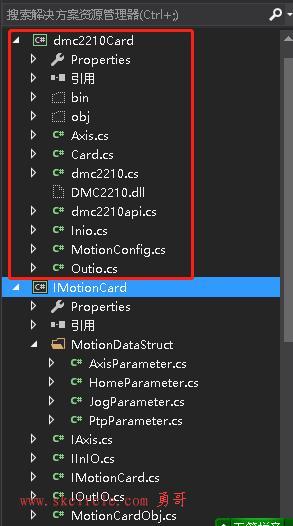
少有人走的路[置顶]python知识导航贴，持续更新
[置顶]C++相关导航贴，持续更新
[置顶]本站连载贴子系列，持续更新中……
[置顶]勇哥的免费视频教程清单
[置顶]勇哥在B站发布的视频清单
[置顶]运动控制专题，持续更新
2020-08-10 09:01:34
坐标旋转变换公式的推导
我们知道autocad中的ucs指令可以变换坐标系，然后可以查询同一个点在不同坐标系下的位置。勇哥想实现这个功能，因此先收集一些资料。1 围绕原点的旋转如下图， 在2维坐标上，有一点p(x, y) , 直线opの长度为r, 直线op和x轴的正向的夹角为a。 直线op围绕原点做逆时针方向b度的旋转，到达p’ (s,t)s = r cos(a + b) = r cos(a)cos(b) – r sin...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:13633 | 评论:0
2020-07-17 17:53:51
沉浸式学习线性代数！这里有一本全交互的线性代数书
今天，我们给大家介绍一本好玩的线性代数书籍。线性代数的书籍那么多，这本却独具特色。准确来讲，量词似乎不能用「本」，因为它需要在网页上阅读，更重要的是，书里的图是可以动的，读者还可以拖动图。这种交互式图看起来很有意思～书籍地址：http://http://immersivemath.com/ila/index.html《Immersive Linear Algebra》的作者是 J. Ström、K...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:4758 | 评论:3
2020-07-17 14:51:31
如何通俗的解释仿射变换？
知乎里有些扫盲贴真是精华，讲得相当通俗易懂。
把复杂的东西讲清楚也是件不容易的事，这篇文章的作者是用了真心。简单来说，“仿射变换”就是：“线性变换”+“平移”。先看什么是线性变换？1 线性变换线性变换从几何直观有三个要点：变换前是直线的，变换后依然是直线直线比例保持不变变换前是原点的，变换后依然是原点比如说旋转1.1 代数简单讲一下旋转是怎么实现的，可以让我们进一步了解代数是怎么描述线性变换的。...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:4599 | 评论:0
2020-07-13 21:51:42
affine transformation matrix 仿射变换矩阵 与 OpenGL
变换模型是指根据待匹配图像与背景图像之间几何畸变的情况，所选择的能最佳拟合两幅图像之间变化的几何变换模型。可采用的变换模型有如下几种:刚性变换、仿射变换、透视变换和非线形变换等，如下图：参考： http://wenku.baidu.com/view/826a796027d3240c8447ef20.html 其中第三个的仿射变换就是我们这节要讨论的。仿射变换(Affine Transformati...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:5101 | 评论:0
2020-07-12 08:44:29
几何变换详解
在三维图形学中，几何变换大致分为三种，平移变换（Translation），缩放变换（Scaling），旋转变换（Rotation）。以下讨论皆针对DirectX，所以使用左手坐标系。平移变换将三维空间中的一个点[x, y, z, 1]移动到另外一个点[x', y', z', 1]，三个坐标轴的移动分量分别为dx=Tx, dy=Ty, dz=Tz, 即x' = x +...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:4198 | 评论:0
2020-07-11 16:54:49
C# Drawing.Drawing2D.Matrix类，二维矩阵几何变换的3x3仿射矩阵类
本文介绍的Matrix，是.net自带的类. 其命名空间为：System.Drawing.Drawing2D注意并不是netMarketing中那个netMarketing.graphics.Matrix在GDI+中，可以在Matrix对象中存储仿射变换。由于表示仿射变换的矩阵的第三列总是（0,0,1），因此在构造Matrix对象时，只需要指定前两列的6个数。语句：Matrix myMatrix...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:9041 | 评论:0
2020-07-11 07:19:04
C# 一个gdi+中应用矩阵进行二维变换图片的例子
Introduction2D image transformation in .NET has been very much simplified by the Matrix class in the System.Drawing.Drawing2D namespace. In this article, I would like to share with the reader on the u...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:4789 | 评论:0
2020-07-10 21:13:13
Android中关于矩阵（Matrix）前乘后乘的一些认识
在上一篇文章中，我们讲到，在Android中，scale（缩放），rotation（旋转）和 translation（平移）都是以矩阵（Matrix）的形式定义的，实际上在图形学中，这些平面图形的变换都是以矩阵的形式存在的。先来回顾一下，下面，左中右分别scale（缩放），rotation（旋转）和 translation（平移）在Android中的矩阵表示：如果只是单纯的应用某一个变换，我们都知...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:4225 | 评论:0
2020-07-10 11:41:05
2D平面中关于矩阵（Matrix）跟图形变换的讲解
在二维平面上，常用的有以下三种基本的图形变化：1）Translation2）Scale3）Rotation在Android的开发中，我们也经常会用到这样的一些图形变换，尤其是我们在写自定义View时，更是会经常利用到Matrix来实现一些效果，比如平移，旋转，缩放及切变等，相信很多朋友应该很想知道，矩阵实现这种变换的原理是什么，什么是矩阵的左乘右乘，它们在实现效果上有什么差别吗？今天就让我们一起来...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:4567 | 评论:0
2020-07-09 17:44:05
二维图形的矩阵变换（一）——基本概念
基本的二维变换可包括旋转、缩放、扭曲，和平移四种，而这些几何运算则可以转换为一些基本的矩阵运算：这几个变换都是线性的，但平移运算不是线性的，不能通过2*2矩阵运算完成。若要将点 (2, 1)在 x 方向将其平移 3 个单位，在 y 方向将其平移 4 个单位。 可通过先使用矩阵乘法再使用矩阵加法来完成此操作。综合这几种基本运算，数学家们将其统一为一个3*3矩阵，存储形式如下：由于表示仿射变换的矩阵的...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:6386 | 评论:0
2020-07-02 21:14:19
【Unity】6.2 在VS2015中调试 C# 脚本
Unity虽然是开发游戏用的，但是可以用来验证视觉原理算法。勇哥折腾了几天，无法运行场景后，让场景对应的C#代码断点断下来，不知道怎么回事。反复的的从4.x版本安装到5.x，还是不行。其实不是Unity的版本问题，是教程没教对头。按照下面这个教程则成功了。一、简介这一节先利用GUI显示一个简单的界面（以后还会专门介绍GUI），并解释如何在VS2015中调试C#脚本。本节例子的运行效果如下：二、调试...
作者:勇哥,很想停止 | 分类:视觉实验 | 浏览:3824 | 评论:2
2020-06-30 09:14:38
几何向量(14)：计算光线反射reflect向量
这一篇我们来聊一下光线反射的基础计算，看过点叉积篇的小伙伴们肯定注意到底下有一句话，就是“为了以后的光线反射reflect计算”，这里我们就别以后以后了，现在就动起来。光线反射是一个非常重要的概念，或者说常识，这里我们来聊一下真实世界。现实世界中，我们眼睛之所以看到各种各样的物体，其原因就是太阳发出的光线照射到地球上，然后经过反射后进入人的眼睛，人的眼睛接收到光子后在视网膜上成像，然后通过生物信号...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:5246 | 评论:0
2020-06-30 09:09:37
几何向量(13)：点与多边形（凸）
国庆放假前写一篇，搞不好整个国庆没得机会写了，在几何开发中，点与凸多边形的关系判断属于很常见的，比如射线与平面相交，判断交点是否在若干顶点组成的多边形中。 和之前判断点在三角形中类似，先来一张点与多边形关系示意图，如下： ①很容易就看的出来，五个夹角之和等于360°，②可以看得出来∠BPC=其他四角之和，除非∠BPC在线段BC上，不然小于180°，则五夹角之和小于360°。...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:3481 | 评论:0
2020-06-30 09:07:07
几何向量(12)：点与三角形
判断点在三角形内部，属于三维开发中很常用的一种算法，之前搞忘记说了，前面我们判断射线与平面，如果再加上判断交点是否在三角形内的计算就更好了。 好，假设我们有个三角形，和三角形所在平面的一个点，那么怎么判断点与三角形的关系，先来个示意图，如下：可以看的出来，如果点P在三角形内部，那么P与三角形ABC组成的六个夹角之和为180°（三角形内角和180°），如果在三角形外部，则不然。...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:4058 | 评论:0
2020-06-30 09:03:42
几何向量(11)：射线与平面
射线与平面的检测属于三维空间典型的检测算法之一，属于三维中基础实用一通百通的技术之一。 之前我们在空间点与平面中已经大致了解了其中的概念和原理，不清楚的可以先回过去看下，空间表示法A*x+B*y+C*z+D = 0，射线表示法为start + n*dir（起点+模长*朝向），那么射线与平面检测，就是解方程组就好了，还是画个图方便理解，如下：程序设计思路也简单，首先使用叉积计算出平面单位...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:4653 | 评论:0
2020-06-30 08:59:47
几何向量(10)：三维点与直线
在三维图形问题中，点和直线计算是很常见的，比如，已知三维空间中一条直线和任意非直线上的点，求点到直线的垂线（或垂点），这个问题比较典型，基本上就属于一系列三维空间点与直线关系的代表。 首先如下图：学到现在的几何向量，一眼就看得出来，只需要根据向量PC1与向量PV的点积等于0，得到方程组就可以最终计算出P点坐标了。首先我们确定三维空间中P点表示法，使用C1 + n*dir的形式，其中C1为起...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:3297 | 评论:0
2020-06-30 08:57:13
几何向量(9)：叉积和夹角（左手定则）
最近又回顾了一遍叉积，概念我们应该了解，几何上就是向量a和b，那么向量a和b的叉积得到向量c，向量c与向量a和b相互垂直，也就是说向量c垂直于向量a和b所在的平面，同时向量c的模长等于向量a和b组成的平行四边形的面积。 物理上叉积的意义就是力矩的意义。 这里回顾一下以前写的叉积篇：叉积 实际上有个重要的问题以前忽视掉了，那就是unity左手坐标系中的叉积计算遵循左...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:4194 | 评论:0
2020-06-30 08:50:07
几何向量(8)：Angle/SignedAngle函数解析
最近又跑去温习基础数序去了，没办法，人对某个事物的永久记忆是七次理解才能达成，所以抽空写一些常用的数学计算。 在二维和三维开发中，计算向量之间夹角属于很常见的操作，在数学中我们可以使用下面： 1.余弦定理，如果我们知道三边的情况下，使用余弦定理可以计算出任意角的角度，如图： 2.点乘（点积），我们可以通过点乘（点积）推导出： a·b...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:6375 | 评论:0
2020-06-30 08:45:55
几何向量(7)：ScreenToViewportPoint/ScreenToWorldPoint函数解析
三维引擎中Camera类带有一系列几何函数，这里我们看一下unity中这两个Camera提供的几何函数的意义和实现： 1.ScreenToViewportPoint 顾名思义就是屏幕坐标转视口坐标，在渲染流程中，建模->世界->视口->裁剪->视图得到屏幕坐标系中坐标数值，那么阶段性反过来从屏幕到视口的坐标变换也好理解，屏幕的左下角（0,0）到右...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:4554 | 评论:0
2020-06-30 08:36:11
几何向量(6)：二维点与直线
这一篇是几何向量的扩展篇之一，因为后面要讲到的CG技术需要这一篇的数学基础，所以额外开一篇进行讲解。 这次我们就观察学习二维中点与直线的重要关系，垂线或者说图形学中的法线，因为这和后续的反射向量、光追计算、镜面计算等有很大依赖关系，比如说我们有一个顶点P处于一块二维镜面前，求这个顶点P在二维镜面中的倒影顶点P'，这就需要求出顶点P到镜面所处的直线L的垂线及距离了，如下图： 首先...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:3390 | 评论:0
2020-06-29 20:45:32
空间向量知识点归纳总结(经典)
二维向量即平面向量，三维向量即空间向量。平面向量是在二维平面内既有方向又只有大小的量，物理学中也称作矢量，与之相对的是只有大小、没有方向的数量（标量）。空间中具有大小和方向的量叫做空间向量。向量的大小叫做向量的长度或模（modulus)。规定，长度为0的向量叫做零向量，记为0。模为1的向量称为单位向量。与向量a长度相等而方向相反的向量，称为a的相反向量。记为-a；方向相等且模相等的向量称为相等向量...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:29340 | 评论:0
2020-06-23 21:49:35
线性代数（7）：仿射变换图形矫正
之前学习完矩阵的理解和作用，又经历过一轮基本仿射变换推导，我想大家对矩阵在实际程序中的应用应该基本了解了，这里我们就实际应用一下。 之前学习的变换过程基本都是变换一个“规范”的图形，这次我们就反过来，把一个“不规范”的图形变换“规范”。 首先作为码农们，我们应该都会阅读大量书籍的，但是为了方便我自己下载过大量pdf文档，因为那样我不需要随身带一本厚重厚重的书，只用带个...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:3811 | 评论:0
2020-06-23 21:44:58
线性代数（6）：矩阵变换图形（三维错切变换）
之前我们学习了理解了图形学中的线性代数，而且实际的操作了图形的基础变换，既然学习完基本变换了，那么接下来就看看一些不常见的特殊变换，下面我们就看看错切变换，也称为切变。 这里要介绍一下仿射变换的一个特点，就是“平直性”，因为前面我们理解仿射变换是一个线性变换加上一个平移，线性这个性质就保证了直线变换后还是直线，所以仿射变换，变换后的图形，是直线边的还是直线边。 切变是一...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:5781 | 评论:0
2020-06-23 21:38:17
线性代数（5）：矩阵变换图形（三维平移缩放旋转）
这篇博文我只是准备对上一篇博文的内容进行扩展，因为上一篇我写完二维xy仿射坐标系的变换，这一篇我就扩充到三维xyz仿射坐标系的变换推导。 前面我们已经理解学习完矩阵在图形学中的作用，所以这一篇我只做纯推导和图形应用演示。 1.矩阵操作三维仿射坐标系平移，如下图： 三维仿射空间平移无非就是xyz三轴移动，建立齐次坐标和4x4矩阵就能推出来...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:5491 | 评论:0
2020-06-23 21:30:58
线性代数（4）：矩阵变换图形（二维平移缩放旋转）
前面我们从理论上理解了图形学中图形的变换过程，具体可以理解为如果要对一个图形A进行变换，那么存在图形A所处的相同原点的仿射空间SpaceA（或者说仿射空间SpaceA中原点处存在一个图形A），这时候我们暂时忽略图形A，只考虑SpaceA经过各种变换最终变换成另一个仿射空间SpaceB（或者说变换后的仿射空间SpaceA与另一个仿射空间SpaceB重合），因为仿射空间SpaceA变换后可能被伸缩...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:6533 | 评论:0
2020-06-23 21:25:42
线性代数（3）：理解齐次坐标
前面有个问题我们还没聊开，不知道小伙伴们记得不？在几何向量的基本概念这一章，我们了解了如下两个概念： 1.矢：空间中的一个直线段，当规定其两个端点中一个为起始点，一个位终止点，这个线段就称为一个矢。 2.向量：具有同样长度和方向的失的集合称为一个向量，单独的一个矢为向量的一个代表。 这里就引出了我们迷惑的问题了，因为数学上（当然程序中也一样）表示向量...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:5567 | 评论:0
2020-06-23 07:02:40
机器视觉常见数学公式回顾（一）
机器视觉常见的数学公式很多，下面的贴子会由浅到深依次跟贴下去，以方便大家查阅与记忆。（一） 6个必须有记住的三角函数公式：（二）直线方程相关（1） 直线斜率 经过两点P1(x1,y1), P2(x2,y2) (x1≠x2)的直线斜率的公式：（2）两点之间的距离 平面坐标空间坐标（3）两点式直线方程（4）直线的一般方程（5）两直线交点例题：（6）点到直线的距离 例题：（7）两条平行线间的距离 （三）...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:6798 | 评论:0
2020-02-22 11:30:18
OpenCV畸变校正原理以及损失有效像素原理分析
上一篇博客简要介绍了一下常用的张正友标定法的流程，其中获取了摄像机的内参矩阵K，和畸变系数D。1.在普通相机cv模型中，畸变系数主要有下面几个：(k1; k2; p1; p2[; k3[; k4; k5; k6]] ，其中最常用的是前面四个，k1,k2为径向畸变系数，p1,p2为切向畸变系数。2.在fisheye模型中，畸变系数主要有下面几个（k1,k2,k3,k4）. 因为cv和fisheye的...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:7423 | 评论:0
2020-02-22 10:51:09
OpenCV亚像素角点cornerSubPixel()源代码分析
上一篇博客中讲到了goodFeatureToTrack（）这个API函数能够获取图像中的强角点。但是获取的角点坐标是整数，但是通常情况下，角点的真实位置并不一定在整数像素位置，因此为了获取更为精确的角点位置坐标，需要角点坐标达到亚像素（subPixel）精度。1. 求取亚像素精度的原理 找到一篇讲述原理非常清楚的文档https://xueyayang.github.io/pdf_posts/%E...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:3355 | 评论:0
2020-02-22 09:55:34
亚像素级点定位及边缘定位算法
在这篇博客里，主要讲解两点：点定位(Point localization)以及边缘定位(Edge localization)，均是亚像素级定位精度。当然还有其他定位方法，这里仅针对亮点和边缘两种情形分别进行精确定位。1. 为何需要进行亚像素定位？>数字图像通常是被离散化成像素形式；>每个像素对应一个整数坐标位置；>整数坐标位置对于很多应用然而并不精确，比如跟踪、相机标定、图像配准...
作者:勇哥,很想停止 | 分类:行业算法与知识 | 浏览:6127 | 评论:0
- 会员中心
- 搜索
- 网站分类
-
- .net程序调试
- 系统架构师
- Remoting
- 消息队列
- WCF/SOA
- C#高级话题
- Xamarin和MAUI
- WinUI3
- asp.net
- 网站前端框架
- webApi
- jQuery
- WebService
- Node.js
- .net core
- MEF
- asp.net core
- EFCore
- blazor
- Canvas
- SignalR
- gRPC
- 源生成器
- web端技术
- 驱动开发
- java
- 工业仿真
- 云计算
- 大数据
- 物联网/工业互联网
- 区块链
- 人工智能
- 虚拟现实和增强现实
- solidworks
- 行业示例源码和资源
- 本站开源软件与资源
- 自定义控件
- 本站原创软件与资源
- OSGI.NET
- Workflow
- 杂七杂八的文章
- 网页自动化技术
- c++/QT/MFC
- 机器人/手眼标定
- 理财知识
- 视觉实验
- netMarketing类库说明档
- 电气与3D图
- OpenCV
- 数据库
- Matlab
- C#/.net框架
- C# 异步编程
- C# TPL
- C#事件与委托
- python
- 工业视觉/halcon
- 面向对象/设计原则/设计模式/代码重构
- 安卓、IOS、Xamarin 开发
- 版本控制
- 哲学与人生
- PLC和单片机技术
- VisionPro
- 行业软硬件
- 行业算法与知识
- 行业新闻与工作经验
- WPF
- 生活记事本
- 分类器、神经网络、深度学习
- 工业相机镜头选型
- halcon标定
- 凌云视觉软件
- SciSmtCam
- ＶisionMaster
- 3d视觉/点云
- 运动控制
- 标签列表
-
- 最新留言
- 热门文章 | 热评文章 | 随机文章
-
- 文章归档
-
- 2025年4月 (1)
- 2025年3月 (8)
- 2025年2月 (9)
- 2025年1月 (11)
- 2024年12月 (23)
- 2024年11月 (40)
- 2024年10月 (23)
- 2024年9月 (5)
- 2024年8月 (26)
- 2024年7月 (52)
- 2024年6月 (64)
- 2024年5月 (55)
- 2024年4月 (13)
- 2024年3月 (19)
- 2024年2月 (7)
- 2024年1月 (6)
- 2023年12月 (20)
- 2023年11月 (30)
- 2023年10月 (3)
- 2023年9月 (1)
- 2023年8月 (8)
- 2023年7月 (3)
- 2023年6月 (2)
- 2023年5月 (3)
- 2023年4月 (1)
- 2023年3月 (10)
- 2023年2月 (35)
- 2023年1月 (8)
- 2022年12月 (66)
- 2022年11月 (52)
- 2022年10月 (11)
- 2022年8月 (7)
- 2022年7月 (9)
- 2022年6月 (18)
- 2022年5月 (4)
- 2022年4月 (6)
- 2022年3月 (2)
- 2021年10月 (4)
- 2021年9月 (26)
- 2021年8月 (2)
- 2021年7月 (60)
- 2021年6月 (15)
- 2021年5月 (11)
- 2021年4月 (3)
- 2021年3月 (12)
- 2021年2月 (23)
- 2021年1月 (38)
- 2020年12月 (69)
- 2020年11月 (88)
- 2020年10月 (51)
- 2020年9月 (9)
- 2020年8月 (17)
- 2020年7月 (42)
- 2020年6月 (63)
- 2020年5月 (59)
- 2020年4月 (88)
- 2020年3月 (79)
- 2020年2月 (144)
- 2020年1月 (42)
- 2019年12月 (82)
- 2019年11月 (122)
- 2019年10月 (34)
- 2019年9月 (13)
- 2019年8月 (16)
- 2019年7月 (46)
- 2019年6月 (2)
- 2019年5月 (17)
- 2019年4月 (45)
- 2019年3月 (59)
- 2019年2月 (12)
- 2019年1月 (25)
- 2018年12月 (41)
- 2018年11月 (78)
- 2018年10月 (80)
- 2018年9月 (28)
- 2018年8月 (13)
- 2018年7月 (75)
- 2018年6月 (37)
- 2018年5月 (1)
- 2018年4月 (1)
- 友情链接
-
- 扫描加本站机器视觉QQ群，验证答案为：halcon
- 点击查阅微信群二维码
- 扫描加勇哥的非标自动化群,验证答案：C#/C++/VB
- 扫描加站长微信：
- 扫描加站长QQ：
- 扫描赞赏本站：
- 留言板:
Powered By Z-BlogPHP 1.7.2
Copyright Your skcircle.com Rights Reserved.
站长QQ:496103864 微信:abc496103864