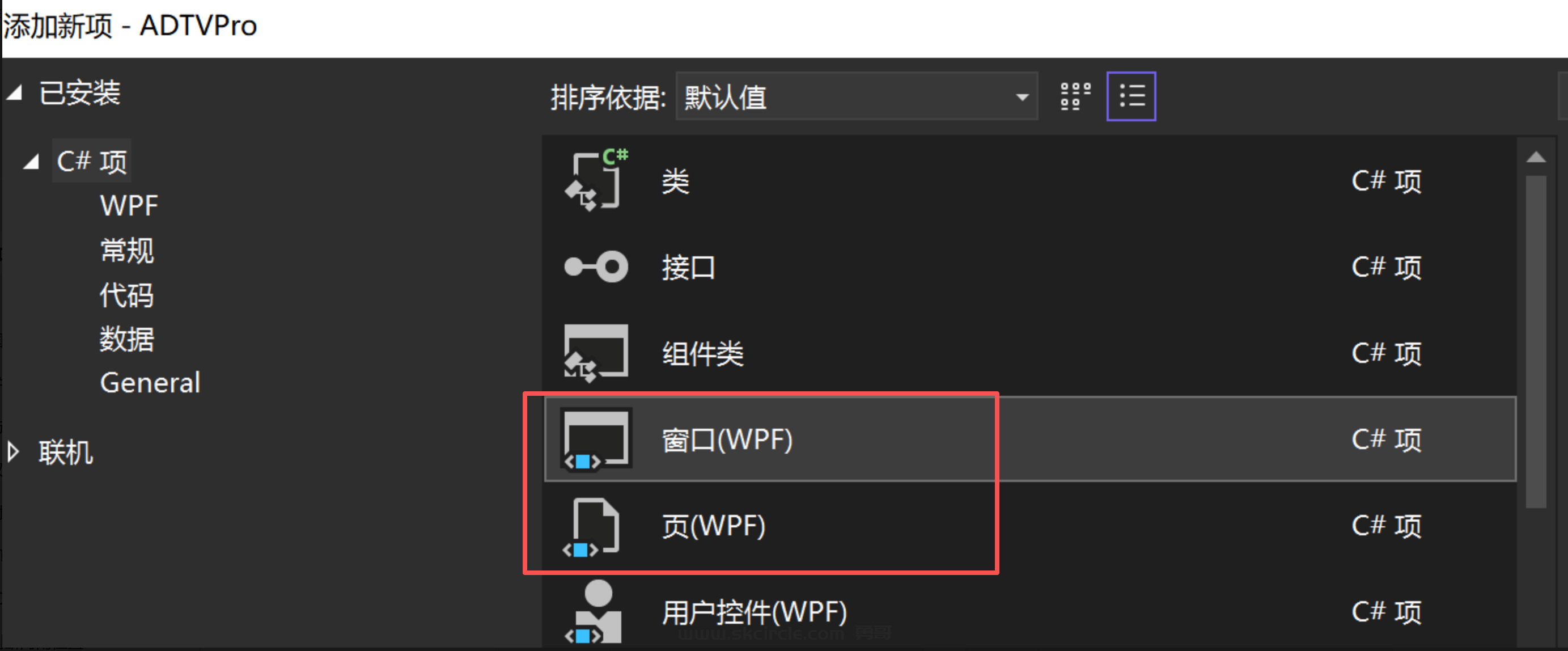
见下面的xaml代码:
<Window x:Class="ADTVPro.MtvMainWindow"
xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"
xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"
xmlns:d="http://schemas.microsoft.com/expression/blend/2008"
xmlns:mc="http://schemas.openxmlformats.org/markup-compatibility/2006"
xmlns:local="clr-namespace:ADTVPro"
mc:Ignorable="d"
Title="MtvMainWindow" Height="450" Width="800">
<Grid>
<TabControl>
<TabItem Header="全部歌曲">
<Grid Background="#FFE5E5E5">
<ListBox x:Name="AllSongsListBox" d:ItemsSource="{d:SampleData ItemCount=5}">
<ListBox.ItemTemplate>
<DataTemplate>
<StackPanel Margin="2">
<TextBlock Text="{Binding SongName}" FontWeight="Bold" FontSize="14"/>
<TextBlock Text="{Binding Pinyin}" FontSize="12" Foreground="Gray"/>
</StackPanel>
</DataTemplate>
</ListBox.ItemTemplate>
</ListBox>
</Grid>
</TabItem>
<TabItem Header="选中的歌曲">
<Grid Background="#FFE5E5E5">
<ListBox d:ItemsSource="{d:SampleData ItemCount=5}"/>
</Grid>
</TabItem>
</TabControl>
</Grid>
</Window>